Атаки ізоморфізму базуються на перетвореннях, що переводять абелеву групу точок в елементи мультиплікативної групи поля. Оскільки, рішення у поле набагато простіше, ніж на еліптичній кривій (при порівнянних порядках), то знаходження ізоморфізму між двома групами істотно знижує безпека ЕСС. Поки відомі кілька класів криптографічно слабких кривих, для яких ці атаки успішні.

2. Метод Шенкса

Прямий метод розрахунку дискретного логарифма може використати два варіанти: - кратне додавання точки до збігу із точкою (шлях від точки до точки ) або шлях від точки до точки. У найгіршому випадку для визначення числа із точки може знадобитися до додавань точки ( при маємо множину зворотних за знаком точок, - координати яких уже відомі). Обчислювальна складність безпосереднього розрахунку дискретного логарифма оцінюється числом операцій . Щоб скоротити шлях до збігу (колізії) з відомою точкою, природно на всьому шляху поставити маркери , , координати яких визначено на етапі попередніх обчислень. Рухаючись від точки до найближчого маркера, ми істотно скорочуємо зону пошуку (рис 1). Виникає лише питання, як розставити маркери?

Рисунок 1 - Подання елементів циклічної групи точками на колі й інтервал аналізу за методом Шенкса

По суті введення маркерів - це обмін обчислень на пам'ять. Якщо об'єми цих ресурсів зробити рівними, то відстань між маркерами слід вибирати рівною . Ця ідея запропонована Д.Шенксом.

Метод Шенкса часто називають методом великих і малих кроків (Giant step-Baby step). Маркери - це Giant step. Номери цих точок з їх -координатами зберігаються в пам'яті. Baby step – це послідовні додавання точок після чого обчислені -координати порівняюються з координатами маркерів. При збігу координат отримуємо , звідки визначається шукане значення . Метод Шенкса є детерміністським.

Обчислювальна складність методу оцінюється як середнє число малих кроків. Основний недолік методу – надмірний об'єм необхідної пам'яті, пропорційний .

Крім того, на кожному кроці порівняння координат здійснюється по всіх точках, що зберігаються в пам'яті. Для задач реального криптоаналізу метод не знайшов застосування. Однак, часто метод Шенкса приводиться як теоретична основа для інших, більш практичних методів рішення .

3. Метод ділення точок на два ( продовження)

Він заснований на використанні точок <P> з максимальним порядком , (коефіцієнт кривої a=0). Задамо рекурентну функцію ділення-відрахування

(1)

Оскільки кожне ділення дає дві точки, повна процедура утворює дерево розв’язків із галузями ( - число віднімань точки ). В ідеальному випадку, при правильному виборі точок ділення, одна з галузей найбільш коротким шляхом веде до точки , а інша – . При цьому двійковий запис алгоритму ділення (0) або відрахування – ділення (1) дає шукане число або . Для цього буде потрібно не більше ділень. Зрозуміло, при випадковому виборі точок ділення ймовірність знаходження таких галузей мізерно мала.

Точки групи <P > зручно подати у вигляді еквідистантних точок кола, починаючи відлік від точки ПРО, розташованої ліворуч за годинниковою стрілкою (рис. 2). Будь-якій парній точці групи <P > ® відповідають дві точки ділення й , розташовані на одній діагоналі кола й пов'язані співвідношенням із точкою другого порядку. Значення точок , верхнього півкола можна розглядати як додатні, а нижнього півкола - як від’ємні. Координати кожної такої пари збігаються, а . У процедурі ділення, що прагне до точки , можна ігнорувати знак точки, зазначимо, що є лише - координата точки. Назвемо "правильною" точкою ділення точку лівого півкола (на рис 2 – точка ). Послідовний вибір "правильних" точок ділення в процедурі веде до точки й, відповідно до розв’язання . Злом криптосистеми, у такий спосіб зводиться до вирішення еквівалентних проблем:

– визначення, у якому пів кола групи <P > перебуває деяка точка цієї групи;

– визначення співвідношення (більше - менше) між двома довільними
точками й групи <P >;

– визначення парності ( непарності) числа для точки ;

– чи виконується редукція за модулем при подвоєнні довільної точки із групи порядку ?

Доки відповісти на ці запитання не вдається ECC залишається стійкою криптосистемою з експоненційною складністю розв’язання . Для криптоаналізу зовсім необов'язково прийти до точки або , достатньо знайти точку з -координатою точки, що раніше зустрічалася в цій процедурі, або будь-якої іншої відомої точки групи <P >. У першому випадку рішення при колізії близько до - методу Полларда, у другому – до методу Шенкса.

Доцільно використовувати максимально можливу кількість інформації (передрозрахунки) з метою збільшення ймовірності колізій, однак це веде до збільшення кількості перевірок і розширення пам'яті.

крива поле дискретний логарифмування атака

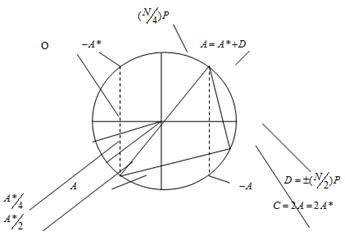
Рисунок 2 - Геометрична ілюстрація методу ділення точок кривої на два

Якщо в 1 залишити лише одну операцію ділення на два з вибором точки із групи 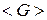, то ітераційна процедура ділення на два в остаточному підсумку також призведе до точки 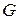(або іншої відомої точки), якщо 2 є примітивним елементом поля 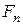. Послідовне ділення точок на два вимагає в НБ лише одне множення в полі на кожному кроці, інші операції практично не вимагають витрат. При цьому, імовірно, можна досягти максимальної швидкості криптоаналізу. Цей метод, однак, рівносильний повному перебору всіх точок. Більш доцільним, можливо, є випадковий пошук колізій зі складністю .

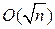4. Аномальні криві й криві над розширеннями малого поля

Аномальні криві над розширеннями поля (криві Коблиця) виду , мають особливості структури групи E , що дозволяють зменшити в раз об'єм аналізованих точок кривої (у порівнянні із групою загальної структури) і, відповідно, у раз обчислювальну складність пошуку колізій. Це пов'язано з виникненням класів еквівалентності точок кривої, породжуваних послідовним піднесенням у квадрат координат вихідної точки.

Позначимо функцію при цьому Для будь-якої точки порядку кривої над полем визначається ендоморфізм Фробеніуса (відображення поля в поле), який задовольняє характеристичне рівняння

Тут операція додавання визначена як додавання в групі E , а параметр називають слідом ендоморфізма Фробеніуса. Зокрема, для кривої Коблиця з коефіцієнтами з поля й параметром маємо

Тому що функція не змінює порядку точки, справедлива рівність , при цьому , а характеристичне рівняння Фробеніуса приймає вигляд