Реферат: Способы улучшения цифровых сигналов в условиях ограниченного объема априорной информации

Анализ зависимостей, представленных на рис. 3, показывает, что импульсная характеристика лежит только в положительной полуплоскости. Следует отметить, что импульсная характеристика быстро спадает, в связи с этим можно ее ограничить и рассматривать на интервале , где составляет 20–25 отсчетов относительно положения единичного скачка. При коэффициентами и можно пренебречь, так как , при .

На рис. 4 представлены нормированные значения результатов, полученных ранее для проведения сравнения величины при различных значениях .

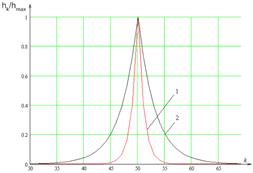
Рис. 4. Сравнение нормированных характеристик при (кривая 1) и при (кривая 2)

Анализ нормированных импульсных характеристик, представленных на рис. 4, показывает, что при увеличении параметра импульсная характеристика становится более пологой.

Для обработки цифровых сигналов по мере поступления данных предлагается обработка входной реализации путем нахождения оценок многокритериальной целевой функции в задаваемом окне с последующим скольжением окна по всем значениям входной реализации.

Выбор величины окна обработки обусловлен минимумом итерационных затрат для получения оценок входной реализации и представлен на рис. 5 при , [7].

а)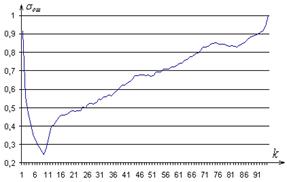

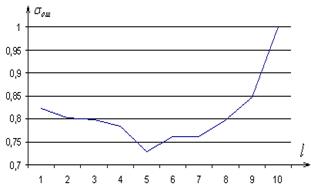
б)

Рис. 5. График изменения значения среднеквадратического отклонения от ширины окна (а) и величины шага перемещения окна (б)

Анализ результатов, представленных на рис. 5, показал, что минимум зависимости достигается при , а – при и слабо зависит от функции полезной составляющей . На рис. 6 представлены зависимости , которые получены при сглаживания исходной реализации (1) многокритериальной целевой функцией, где в качестве обрабатываемых значений использовались сигналы, огибающие которых описываются: составной моделью (кривая 1), треугольной формой (кривая 2), экспоненциальной функцией (кривая 3), параболической функцией (кривая 4), а также гармонической формы (кривая 5), при этом аддитивный шум гауссовского закона распределения [8].

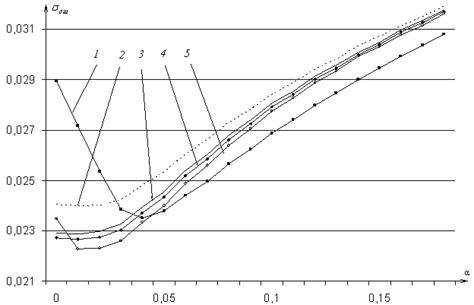
Рис. График выбора параметра

Анализ результатов, представленных на рис. 6, показал, что использование двухкритериальной целевой функции вида (6) позволяет локализовать значение параметра на одном участке (табл. 1) при обработке реализаций сигнала с различными функциями . Погрешность в выборе параметра приводит к увеличению значения до 10 %.

В табл. 1 приведены значения параметра , при котором значения среднеквадратической погрешности являются минимальными, значения [3].

Таблица 1 Минимальная среднеквадратическая погрешность

сигнал иссле дуемый параметр	Составная модель полезного сигнала	сигнал треугольной формы	экспоненциальная функция	параболическая функция	гармоническая функция
	0,04	0,02	0,01	0,01	0,01
	0,023502	0,023961	0,022876	0,022665	0,022271
	0,21	0,08	0,08	0,09	0,21
	0,025858	0,026778	0,032578	0,03423	0,041156

Процесс получения оценок в скользящем окне параметра осуществляется параллельной обработкой исходных значений, находящихся в обрабатываемом окне, многокритериальной целевой функцией с различными параметрами обработки . Правило выбора параметра представлено в работе [2, 3]. Переход между оценками, полученными с различными параметрами , осуществляется условием:

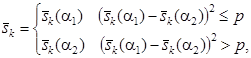
где , – оценки входной реализации, полученные при параметрах и , p – пороговое значение, определенное экспериментально при дисперсии аддитивной шумовой составляющей , составляет .

На рис. 7 представлен пример обработки цифрового сигнала (кривая 1) представленного в виде аддитивной смеси (1) полезного сигнала (кривая 2) и шумовой составляющей при наличии импульсных помех [8].

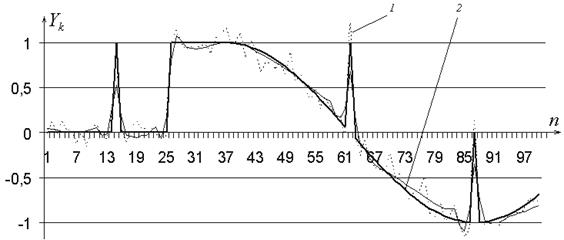
Рис. 7. Пример сглаживания цифрового сигнала при наличии импульсных помех с последующим прогнозированием

цифровой сигнал шум априорная

выводы

1. Разработаны и исследованы многокритериальные методы сглаживания цифровых сигналов в условиях ограниченного объема априорной информации о функциях сигнала и статистических характеристиках шума.

2. Использование многокритериальных методов сглаживания для обработки цифровых сигналов в скользящем окне, показало их высокую эффективность, в среднем на 25 %, в сравнении с обработкой всей реализации. При наличии во входной реализации функций разрыва первого рода или скачков единичной амплитуды происходит повышение эффективности в среднем на 60 %, в сравнении с используемыми на практике аналогами, в качестве критерия эффективности используется среднеквадратическое отклонение оценок от значений входной реализации.

Библиографический список

1. Марчук В.И. Сравнение результатов решений двухкритериальных целевых функций. / В.И. Марчук, Е.А. Семенищев // Наука и образование без границ: материалы 3-й междунар. научно-практич. конф. Т. 1 Технология. – София : «Бял ГРАД-БГ» ООД, 2007. – С. 80–82.