Реферат: Статистическое изучение модификационной изменчивости. Построение вариационных рядов
В нашем примере
4 ![]()
Определить условное отклонение (а ) каждого класса от нулевого путем вычитания порядкового номера нулевого класса от порядкового номера других классов. Вверх от класса, принятого за условный нулевой, получим натуральный ряд отрицательных чисел (–1, –2, –3 и т.д.), вниз – натуральный ряд положительных числе (+1, +2, +3 и т.д. в зависимости от класса).
5 Найти произведение частоты на условное отклонение для каждого класса (ра ) и заполнить графу.
6 Найти сумму частот (Sр = n = 50).
7 Вычислить сумму произведений частот на условное отклонение. Она равна:
Sра = –25+34 =9.
8 Вычислить среднее арифметическое по формуле:
![]()
где А – условное среднее значение нулевого класса;
i – величина классового промежутка.
![]()
Таким образом, средний вес равен 53,5 кг.
Показатели изменчивости
![]()
Средние величины характеризуют всю выборку в целом. Но основное свойство ее членов – свойство изменяться от особи к особи – остается при этом нераскрытым.
Для суждения о степени изменчивости или вариабельности признаков в биометрии наиболее часто используются следующие показатели:
– лимит или размах изменчивости;
– среднее квадратическое или стандартное отклонение;
– коэффициент вариации или изменчивости.
Лимит или разница между максимальным и минимальным значениями признака в выборке является наиболее простым, но и наиболее точным способом количественного выражения степени изменчивости этого признака.
Например, вес спортсменов max = 67 кг, min = 42, lim = 67–42 = 25 кг.
Основным показателем изменчивости является среднее квадратическое отклонение. Среднее квадратическое или стандартное отклонение – это статистическая величина, которая показывает, насколько признак, присущий данному варианту, отклоняется от средней арифметической для данной выборки.
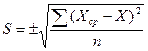 |
??????? ?????????????? ?????????? ?????????? ???? ????????? ?????? S, ???? ?????. ??? ????? ??????? ??????? ?????????????? ?????????? ????????? ?? ??????? :
Вычисление среднего квадратического отклонения для малых выборок производят в следующем порядке:
1 Находят отклонение каждого варианта от средней арифметической для данной выборки, т.е. устанавливают центральные отклонения.
2 Центральные отклонения возводят в квадрат, чтобы избавиться от отрицательных чисел.
3 Находят сумму квадратов.
Пример. Представлена совокупность, состоящая из 5 особей. Все они имеют одинаковый возраст и относятся к одной группе. Нужно вычислить среднюю длину их тела и среднее квадратическое отклонение этого признака.
1. Составим простой вариационный ряд (табл.3)
Таблица 3
| Показатели вариационного ряда | Особи №1 №2 №3 №4 №5 | Статистические показатели |
| Варианты ряда (длина тела в см) | 45 40 38 35 32 |
Средняя арифметическая Х ср = 38 см |
| Отклонение каждой варианты от средней арифметической X–Xср | +7 +2 0 –3 –6 |
Сумма всех отклонений К-во Просмотров: 357
Бесплатно скачать Реферат: Статистическое изучение модификационной изменчивости. Построение вариационных рядов
|