Реферат: Статистическое изучение модификационной изменчивости. Построение вариационных рядов

Квадраты отклонений

(X–X_ср )²

49 4 0 9 36 Сумма квадратов отклонений S (Х –Х_ср )² = 98

2. Вычислим среднюю арифметическую Х:

3. Вычислим отклонения размеров длины тела от средней арифметической

(Х–Х_ср ) и полученные данные проставим в таблицу.

4. Так как сумма отклонений всегда равна нулю S (Х–Х_ср ) = 0, то отклонения следует возвести в квадрат и определить сумму квадратов отклонений. В данном примере они будут равны:

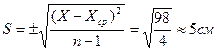S (Ֆ?_ср )² = 49+4+0 + 9 + 36 = 98;

Вычисление среднего квадратического отклонения

для больших выборок

Задание. Вычислить среднее квадратическое отклонение (S) для данной группы спортсменов по весу

1 Составить вариационный ряд (табл. 4).

2 Определить частоту (р) значений веса в каждом классе.

3 Найти условные отклонения (а) от условного среднего класса.

4 Найти произведение частоты на условное отклонение (графа 5).

5 Условное отклонение возвести в квадрат (графа 4).

6 Вычислить произведение частоты на квадрат условного отклонения (графа 6).

7

?? ??????? ????????? ??????? ?????????????? ??????????:

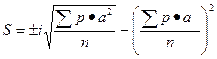Таблица 4

Вычисление среднего квадратического отклонения

Границы классов ( Wн –Wв )	Частоты (р)	Условные отклонения
		(а)	(а)2	ра	ра2
42 –45	1	–3	9	–3	9
46 –48	5	–2	4	–10	20
49 – 51	12	–1	1	–12	12
52 – 54	14	0	0	0	0
55 – 57	8	1	1	8	8
58 – 60	6	2	4	12	24
61 – 63	2	3	9	6	18
64 – 67	2	4	16	8	32
Sр = n = 50	Sра = 9	Sра2 = 123

Нужно обратить внимание на то, что S имеет два знака (+ и –). Это свидетельствует об отклонении вариант от средней арифметической как в положительную, так и в отрицательную сторону. Среднее квадратическое отклонение является показателем разнообразия признака. Согласно правилу 3 S почти все варианты должны укладываться в интервал от –3 S до +3 S, если минимальный вариант (min вес ) не ниже Х–3S, а максимальный (max вес) не выше Х_ср +3 S, то наблюдения ведутся над однородной генеральной совокупностью.

В нашем примере Х_ср + 3 S = 53,5 + 14,04 = 67,54

Х_ср – 3 S = 53,5 – 14,04 = 39,46

Как видим, минимальный вариант 42 не ниже Х – 3 S , т.е. 39,46, а максимальный вариант 67 не превышает Х=3 S, т.е. 67,64. Таким образом, выборка однородна, и изучаемые особи относятся к одному вариационному ряду. Среднее квадратическое отклонение выражается в тех же единицах, которыми измеряется признак, т.е. является поименованной величиной.

Коэффициент изменчивости (вариации)

Основное достоинство среднего квадратического отклонения заключается в том, что оно дает полную количественную характеристику изменчивости изучаемого показателя. Однако сравнить изменчивость двух групп с разными средними значениями изучаемого признака и, тем более, изменчивость разных признаков с помощью данного показателя нельзя. Вот здесь на помощь и приходит следующий показатель изменчивости – коэффициент изменчивости или вариации.

Коэффициент изменчивости характеризует изменчивость в относительных величинах. Это отношение среднего квадратического отклонения к средней арифметической для данной выборки, выраженное в процентах. Коэффициент изменчивости определяется по формуле:

где C_v – коэффициент изменчивости;

S – среднее квадратическое отклонение;

Х_cp – средняя арифметическая.

Вычислить C_v для изучаемых Вами признаков. В нашем примере: