Реферат: Структура графа состояний клеточных автоматов определённого типа
§ 3.3.1 Исследование структуры
Пользуясь утверждением 3.2.2, мы получаем, что среди всех последовательностей можно выделить следующие:
1. которые невозможно получить не из каких других, например: (1,0,0) (они будут образовывать висячие вершины графа);
2. которые, спустя несколько итераций возвращаются в начальное положение, например:
(1,0,0,0) ® (0,1,0,0) ® (1,0,1,0) ® (0,0,0,1) ® (0,0,1,0) ® (0,1,0,1) ® (1,0,0,0)
(такие последовательности в графе будут соответствовать вершинам цикла)
Используя утверждение 3.2.2, можно сделать вывод:
Теорема 3.3.1.1
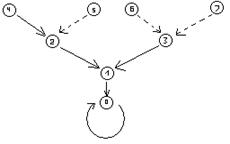
Каждая компонента связности графа 
является циклом (возможно длины 1), каждый элемент которого притягивает дерево (т.е. является корнем ориентированного дерева) (см. рис. 3.2.1).
Наша основная задача определить длины циклов и высоты деревьев, описать их структуру и найти их количество.
|
Теорема 3.3.1.2
Для любых последовательностей k и l, находящихся на одном ярусе какого-то дерева, для которых выполняется условие:
верно равенство:
, где 
―одна из последовательностей «нулевого» дерева на n-ном ярусе.
Более точно это можно сформулировать так:
Рис. 3.2.2
Для любого «полного» корневого поддерева g с корнем v дерева G (с корнем в 
): 
, где 
и 
– подмножество 
такое, что: 
, при этом 
(см. рис. 3.2.2).
Доказательство
Воспользуемся методом математической индукции:
1. m = 1:
Пусть 
, тогда 
. Тогда, учитывая утверждение 1.1, 
и 
, получим требуемое.
2. Пусть утверждение леммы верно для m = k, тогда:
3. Докажем теорему для m = k+1.
Мы имеем: 
, тогда:
Если 
и 
, то
:
Из утверждения 3.2.1:
, но 
, т.е. 
, откуда 
, ч.т.д.
