Реферат: Структура графа состояний клеточных автоматов определённого типа
Доказательство:
Пусть у нас есть последовательности 
и 
Тогда 
Но тогда 
.
Но по условию 
, т.е. для того чтобы вершина 
была висячей необходимо и достаточно, чтобы 
, т.е.
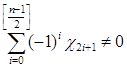
Теорема полностью доказана.
Теорема 3.4.1
Если длина последовательности кратна двум, то граф Gφ ― дизъюнктное объединение циклов.
Доказательство:
Воспользуемся тем, что дерево, притягиваемое каждой точкой каждого цикла, изоморфно нулевому дереву. Рассмотрим нулевое дерево. Его высота при n=2k равна нулю. Это следует из того, что 
, но m=2s+1, противоречие. Теорема полностью доказана.
Теорема 3.4.2
Если длину последовательности представить в виде pk (2l)-1, (p,l)=1, тогда pk есть высота «нулевого» дерева.
Доказательство:
Для начала докажем следующие леммы.
Лемма 1
– висячая вершина причем, 
.
Рис. 3.4.1 Пример для p = 5.
Доказательство леммы 1:
Для начала рассмотрим шахматную раскраску таблицы (2pk -1)(pk +1), строки которой есть последовательности 
, 
, …, 
(см. рис.). Тогда числа, стоящие на закрашенных позициях равны 0.
Остальные координаты образуют треугольник Паскаля с вершиной в 1 (см. пример на рис. 3.4.1 для p = 5). Тогда т.к.
, то:
,
при этом 
(все значения биноминальных коэффициентов берутся по модулю p, так как мы рассматриваем вектор в пространстве 
)
Замечание:
Здесь и ниже, все многочлены рассматриваются над полем 
Докажем, что 
Действительно, т.к.
(т.к. 
), то: 
.
Откуда 
, ч.т.д.
Замечание