Реферат: Структура графа состояний клеточных автоматов определённого типа

Следствие

– висячая вершина причем, .

Для доказательства домножим элементы рассмотренного выше треугольник Паскаля на i и в силу простоты p получим требуемое.

Лемма 2

Вершина н вида:

является висячей при условии, что число последовательностей вида , где не кратно p, причем .

Доказательство леммы 2:

Из теоремы 3.4.0, вершина является висячей при n нечётном и выполнении условия:

.

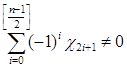Таким образом, при подстановке соответствующих значений получим:

.

, где .

Таким образом, вершина вида:

является висячей при условии, что число конструкций вида , где m=1 либо (p-1), не кратно p. Вторая часть леммы следует из следствия леммы 1, причем, как и в лемме 1, Лемма доказана.

Приступим теперь к доказательству основной теоремы. Из леммы 1 следует, что высота дерева при равна p^k , из леммы 2 следует, что если высота дерева при равна высоте дерева при и, при условии, что (l,p)=1.

Теорема полностью доказана.

§4 Структура графа состояний оператора взятия разностей

Введение

В данном параграфе рассматривается структура графа состояний G_w оператора взятия разностей (см. [1]), который определяется следующим образом:

В ([1]) w был рассмотрен только над Z₂ , в этом параграфе оператор взятия разностей будет рассмотрен над полем Z_p . Оператор взятия разностей используется для анализа сложности функций (см. [1]).

На основе результатов параграфа 2 (теоремы 2.2, 2.3), для анализа структуры графа состояний оператора w достаточно определить высоту нулевого дерева, тем самым будут определена высота дерева притягиваемого каждой точкой каждого цикла графа G_w (теорема 2.3).

Теорема 4.1

Если , то наименьший период функции (modp) по i равен p^k .

Доказательство

Проверим сначала, что число p^k является периодом при :