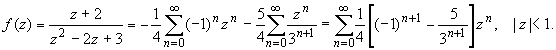Реферат: Теорема тейлора
где ![]()
![]()
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 3 . Разложить по степеням z функцию ![]()
Дробь правильная. Раскладываем ее на элементарные дроби:
![]()
Раскладываем элементарные дроби по степеням z :
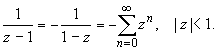
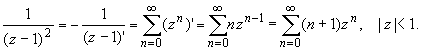
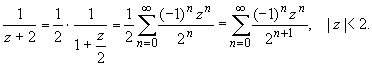
Для исходной дроби получаем разложение:
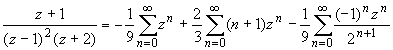
или, складывая ряды:
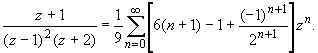
Окончательный ответ:
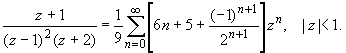
Теорема Лорана (о разложении функции в ряд по целым степеням).
Функция f (z ), аналитическая в кольце
r < | z - z 0 | < R , ![]()
представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство: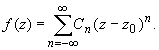 (1)
(1)
Коэффициенты ряда вычисляются по формуле: 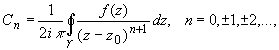 (2)
(2)
где ![]() - произвольный контур, принадлежащий кольцу и охватывающий точку z 0 ; в частности,
- произвольный контур, принадлежащий кольцу и охватывающий точку z 0 ; в частности, ![]() - окружность
- окружность ![]()
Ряд (1), коэффициенты которого вычисляются по формуле (2), называется рядом Лорана функции f (z ).
Совокупность членов ряда с неотрицательными степенями 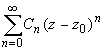 называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана:
называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана: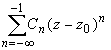 или
или 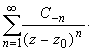
Для коэффициентов ряда имеет место формула оценки коэффициентов - неравенство Коши:![]() где
где ![]()
r - радиус контура интегрирования в формуле (2).
На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f (z ) - его суммы.
Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z 0 (r = 0) и в окрестности бесконечно удаленной точки (z 0 = 0, ![]() ).
).
При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами.
Пример 1. Разложить функцию ![]() в ряд Лорана по степеням z .
в ряд Лорана по степеням z .
Решение. Так как функция является рациональной дробью, то особыми точками являются нули знаменателя, т.е. z 1 = -1 и z 2 = 3. Запишем функцию в виде![]()
Кольца аналитичности | z | < 1, 1 < | z | < 3, | z | > 3.
Раскладываем дробь на элементарные дроби:![]()
При | z | < 1 имеем: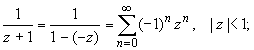
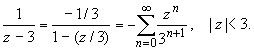
Таким образом, в круге | z | < 1 функция раскладывается в ряд Тейлора: