Реферат: Теорема тейлора

Теорема Тейлора (о разложении функции в степенной ряд).

Функция, аналитическая в области комплексных чисел D , в окрестности каждой точки z ₀ этой области представляется в виде степенного ряда :
(1)

радиус сходимости R которого не меньше, чем расстояние от точки z ₀ до границы области D .
Такой степенной ряд называется рядом Тейлора.

Коэффициенты ряда Тейлора вычисляются по формуле:

(2)

где - произвольный контур, принадлежащий области D и охватывающий точку z ₀ (в частности, - окружность ), или по формуле:

(3)

Радиус сходимости ряда Тейлора равен расстоянию от точки z ₀ до ближайшей особой точки функции.

Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы:

Основные разложения.

(z принадлежит области комплексных чисел);

(z принадлежит области комплексных чисел);

(z принадлежит области комплексных чисел);

(z принадлежит области комплексных чисел);

(z принадлежит области комплексных чисел);

Пример 1 . Записать разложение по степеням z функции f (z ) = ch z .

Найдем производные функции:
f ⁽ⁿ⁾ (z ) = ch⁽ⁿ⁾ z = ch z при n= 2k ,
f ⁽ⁿ⁾ (z ) = ch⁽ⁿ⁾ z = sh z при n = 2k -1.

В данном примере z ₀ = 0. По формуле (3) имеем:
C_n = 0 при n = 2k ; C_n = 1/n ! при n = 2k- 1;
.

Так как ch z - аналитическая функция в области действительных чисел, то радиус R равен бесконечности. В результате имеем:
(z принадлежит области действительных чисел).

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 2 . Разложить по степеням (z -3) функцию f (z ) = sin z .

Обозначим z -3 = t . Используя тригонометрическую формулу для функции sin (3+t), получим:
sin(3+t ) = sin3 cos t +cos3 sin t .

Используя основные разложения, имеем:

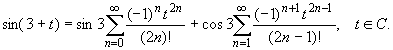
Так как t = z -3, то

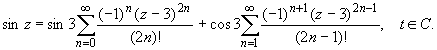
--> ЧИТАТЬ ПОЛНОСТЬЮ <--