Реферат: Теоретическая механика
(2.2)
Модуль полной скорости точки при прямоугольной системе координат будет равен
(2.3)
Направление вектора скорости определяется косинусами направляющих углов
где 
- углы между вектором скорости и осями координат.
Определение скорости точки в естественной системе отсчета
Скорость точки в естественной системе отсчета определяется как производная от закона движения точки
V =
(2.4)
Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях 
nb определяется только одной проекцией 
.
Ускорение точки
По определению ускорение характеризует изменение скорости, т.е. скорость изменения скорости.
Ускорения точки в векторной системе отсчета
На основании свойства производной
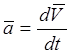, (2.5 )
Вектор скорости может изменяться по модулю и направлению. Для определения приращения вектора 
совместим начала векторов 
(рис.2.6). Вектор ускорения направлен по линии приращения вектора скорости, т. е. В сторону искривления траектории.
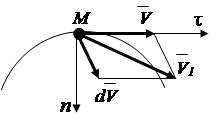
Рис.2.6
Ускорение точки в координатной системе отсчета
Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат
ax =
; ay =
; az =
.
Полное ускорение в прямоугольной системе координат будет определяться выражением
а = 
, (2.6)
Направляющие косинусы вектора ускорения
.
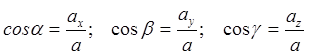Ускорение точки в естественной системе отсчета
Приращение вектора скорости
(рис.2.7) можно разложить на составляющие, параллельные осям естественной системы координат
, (2.7)
Разделив левую и правую части равенства (2.7 ) на dt , получим,