Реферат: Теоретическая механика

где: 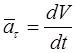- тангенциальное ускорение, (2.9)

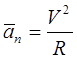- нормальное ускорение, (вывод см .[1], п.43)

где R - радиус кривизны траектории в окрестности точки

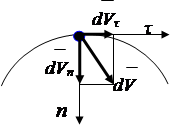Рис. 2.7

2.3. Кинематика твердого тела

В отличие от кинематики точки в кинематике твердых тел решаются две основные задачи:

- задание движения и определение кинематических характеристик тела в целом;

- определение кинематических характеристик точек тела.

Способы задания и определения кинематических характеристик зависят от типов движения тел.

В настоящем пособии рассматриваются три типа движения: поступательное, вращательное вокруг неподвижной оси и плоско-параллельное движение твердого тела

2.3.1. Поступательное движение твердого тела

Поступательным называют движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению (рис.2.8).

Доказана теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения (рис.2.8).

Вывод: Поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.

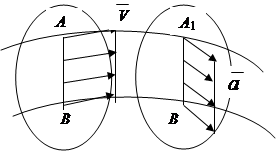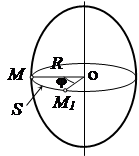
Рис. 2.8 Рис. 2.9

2.3.2 Вращательное движение твердого тела вокруг неподвижной оси.

Вращательным вокруг неподвижной оси называют движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.

Положение тела определяется углом поворота j (рис.2.9 ). Единица измерения угла – радиан. (Радиан - центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2p радиана.)

Закон вращательного движения тела вокруг неподвижной оси j = j(t). Угловую скорость и угловое ускорение тела определим методом дифференцирования

- угловая скорость, рад/с; (2.10)

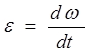- угловое ускорение, рад/с² (2.11)

При вращательном движении тела вокруг неподвижной оси его точки, не лежащие на оси вращения, движутся по окружностям с центром на оси вращения.

Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точка М, то точка М будет описывать вокруг точки С окружность радиуса R (рис. 2.9). За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .Определим модуль линейной скорости:

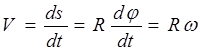( 2.12 )

Ускорение точки М при известной траектории определяется по его составляющим, см.(2.8)

,

где: ; .

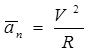Подставляя в формулы выражение (2.12) получим: