Химия / Реферат: Теория химико-технологических процессов

Реферат: Теория химико-технологических процессов

Таблица 3.3. Расчётная таблица для базового опыта.

i τi αi (τi )2 τi αi
1 9000 0,235566 81000000 2120,095
2 18000 0,419124 324000000 7544,232
3 27000 0,662714 729000000 17893,29
4 36000 0,860113 1296000000 30964,07
5 45000 1,070329 2025000000 48164,82
6 54000 1,322055 2916000000 71390,98
7 63000 1,515984 3969000000 95507
8 72000 1,733948 5184000000 124844,3
Сумма: - - 16524000000 398428,8

Отсюда по формуле (3.14):

3.3.2. Оценка дисперсии воспроизводимости.

Её можно произвести по двум параллельным выборкам (опытам 5, 6) с учетом того, что в выборках одинаковое число членов по следующей формуле (3.15) [1]:

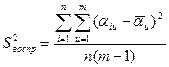(3.15)

Где - ошибка опыта, 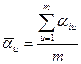, n – количество членов параллельной выборки, m – количество параллельных опытов. При этом число степеней свободы равно .

Т.к. изучается единый технологический процесс, протекающий на одной и той же установке, и так как нет резко выделяющихся значений, то не будем проверять однородность и нормальность результатов параллельных опытов, используя статистику.

Проверка осуществляется по общей схеме проверки гипотез. Для условий базового опыта (t=80ºС, СA, O =1,0 моль/л, СY -, O =0,5 моль/л), при n = 8, т.е. τ1 = 8900, τ2 = 17800, …, τ8 =71200, и m = 2 (число параллельных опытов) получены следующие данные и из них получены выражения для расчета дисперсии воспроизводимости. Все они сведены в таблице 3.4.

Таблица 3.4. Расчётная таблица для дисперсии воспроизводимости базового опыта.

i τi Опыт 5 Опыт 6 Опыт 5 Опыт 6
CY -,i αi CY -,i αi
1 8900 0,406 0,219078 0,403 0,227278 0,223178 0,0041 1,68∙10-5 0,0041 1,68∙10-5
2 17800 0,336 0,436741 0,343 0,412179 0,42446 0,0122 0,000151 0,0122 0,000151
3 26700 0,281 0,658147 0,282 0,653601 0,655874 0,0022 5,16∙10-6 0,0022 5,16∙10-6
4 35600 0,242 0,854529 0,243 0,848975 0,851752 0,0027 7,71∙10-6 0,0027 7,71∙10-6
5 44500 0,205 1,084081 0,208 1,063518 1,073799 0,0102 0,000105 0,0102 0,000105
6 53400 0,178 1,288433 0,176 1,305124 1,296778 0,0083 6,96∙10-5 0,0083 6,96∙10-5
7 62300 0,154 1,506015 0,151 1,536165 1,52109 0,0150 0,000227 0,0150 0,000227
8 71200 0,135 1,710406 0,133 1,733948 1,722177 0,0117 0,000138 0,0117 0,000138
Сумма: - - - - - - - 0,000721 - 0,000721

Отсюда по формуле (3.15) дисперсия воспроизводимости равна:

Число степеней свободы .

3.3.3. Проверка адекватности кинетической модели базового опыта.

Проверим модель на адекватность, т.е. ответим на вопрос: можно ли использовать полученное уравнение регрессии или необходима более сложная модель.

а) Для начала нужно найти по формуле (3.16) дисперсию адекватности:

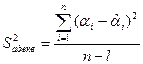(3.16)

В нашем случае n = 8, а количество значимых коэффициентов уравнения регрессии l = 1. найдём по формуле (3.13): . Все данные сведены в таблицу (3.5):

Таблица 3.5. Расчётная таблица для дисперсии адекватности базового опыта.

i
1 0,235566 0,217009 0,018557 0,000344
2 0,419124 0,434018 0,014894 0,000222
3 0,662714 0,651027 0,011687 0,000137
4 0,860113 0,868037 0,007923 6,28∙10-5
5 1,070329 1,085046 0,014716 0,000217
6 1,322055 1,302055 0,020001 0,0004
7 1,515984 1,519064 0,00308 9,49∙10-6
8 1,733948 1,736073 0,002125 4,51∙10-6
Сумма: - - - 0,001396

Тогда по уравнению (3.16):

Число степеней свободы при этом .

б) Проверку адекватности уравнения регрессии эксперименту проводиться по критерию Фишера по формуле (3.17):

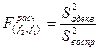(3.17)

Для нашего случая:

Для p= 0,05 по табличным данным [1] найдём, что . Таким образом, т.к. , то гипотеза об адекватности принимается.

3.3.4. Оценка средней квадратичной ошибки коэффициента уравнения регрессии.

По формуле (3.18) имеем:

К-во Просмотров: 314
Бесплатно скачать Реферат: Теория химико-технологических процессов