Реферат: Теория химико-технологических процессов

И следовательно:

3.3.5. Проверка значимости коэффициента уравнения регрессии.

Используя критерий Стьюдента (t_j ), проверим значимо ли kотличается от нуля. По формуле (3.19) можно найти расчётный критерий Стьюдента для k:

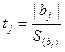(3.19)

В нашем случае уравнение (3.19) имеет следующий вид:

Для p = 0,05 и по таблице квантилей распределения Стьюдента [1] t_0,05 (8) = 2,31. А т.к. t_j > t_0,05 (8), то нулевая гипотеза отвергается, и следовательно kявляется значимым в уравнении регрессии. Подставив значение kв формулу (3.13), получим линейную кинетическую модель реакции: .

3.3.6. Нахождение доверительного интервала для k по данному уравнению регрессии для базового опыта.

Найдём доверительный интервал для kпо данному уровню значимости p = 0,05. Для этого используем формулу (3.20):

(3.20)

В нашем случае для k = 2,41121∙10^-5 ; t_0,05 (8) = 2,31; S_k = 7,75986∙10^-8 . Тогда t_0,05 (8)∙S_k = 2,31∙7,75986∙10^-8 = 1,79253∙10^-7 . Получили:

Вывод:

Уравнением можно пользоваться в пределах эксперимента для описания данной реакции. Поскольку она адекватно описывает опытные данные и хорошо согласуется с экспериментом.

Таким образом, найдена кинетическая модель для описания изучаемой реакции при постоянной температуре. Она имеет вид:

где D – доверительный интервал константы. Тогда:

.

3.3.7. Определение влияния температуры на константу скорости реакции.

Для выяснения влияния температуры на константу скорости реакции, описанным ранее способом находим значение констант скорости при температурах опытов 7, 8, 9:

а) При температуре t=80ºС, С_{A, O} =1,0 моль/л, С_Y -_{, O} =0,5 моль/л, τ₁ = 8900, τ₂ = 17800, …, τ₈ =71200 были получены такие данные:

Таблица 3.6. Результаты опыта 7, приведённые для линейной функции (3.11).

i	τi			αi
1	8900	0,911	0,902305	0,205605
2	17800	0,842	0,812352	0,415644
3	26700	0,781	0,71959	0,658147
4	35600	0,736	0,641304	0,888502
5	44500	0,708	0,587571	1,063518
6	53400	0,675	0,518519	1,313559
7	62300	0,651	0,463902	1,536165
8	71200	0,634	0,422713	1,722124

Таблица 3.7. Расчётная таблица для опыта 7.

i	τi	αi	(τi )2	τi αi
1	8900	0,205605	79210000	1829,885
2	17800	0,415644	316840000	7398,467
3	26700	0,658147	712890000	17572,51
4	35600	0,888502	1267360000	31630,68
5	44500	1,063518	1980250000	47326,54
6	53400	1,313559	2851560000	70144,05
7	62300	1,536165	3881290000	95703,1
8	71200	1,722124	5069440000	122615,2
Сумма:	-	-	16158840000	394220,5

Отсюда по формуле (3.14):

Таблица 3.8. Расчётная таблица для дисперсии адекватности опыта 7.

• «
• 1
• 2
• 3
• 4
• 5
• 6
• »

• >>> Скачать <<<

i
1	0,205605	0,21713	0,011525	0,000133
2	0,415644	0,434259	0,018615	0,000347
3	0,658147	0,651389	0,006758	4,57∙10-5
4	0,888502	0,868518	0,019984	0,000399
5	1,063518	1,085648	0,02213	0,00049