Реферат: Тождественные преобразования выражений и методика обучения учащихся их выполнению

Применим формулу сокращённого умножения:

(101-1) (101+1)=100102=102000

5) Найти значение выражения:

Для нахождения значения домножим каждую дробь на сопряжённый:

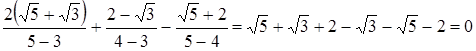
6) Построить график функции:

Выделим целую часть: .

Предупреждение ошибок при выполнении тождественных преобразований может быть получено путём варьирования примеров выполнения их. В этом случае отрабатываются «мелкие» приёмы которые как составные части входят в более объёмный процесс преобразования.

Например:

.

В зависимости от направлений уравнения можно рассмотреть несколько задач: справа налево умножение многочленов; слева направо -разложение на множители. Левая часть кратна одному из сомножителей в правой части и т.д.

Кроме варьирования примеров, можно воспользоваться проведением апологии между тождествами и числовыми равенствами.

Следующий приём – объяснение тождеств.

Для повышения интереса учащихся можно отнести отыскание различных способов решения задач.

Уроки по изучению тождественных преобразований станут интереснее, если их посвятить поиску решения задачи .

Например: 1) сократить дробь:

3) доказать формулу «сложного радикала»

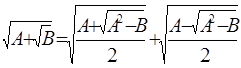
Рассмотрим:

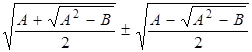
Преобразуем правую часть равенства:

-

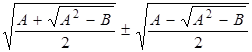сумма сопряжённых выражений. Их можно было бы домножить и разделить на сопряжённый, но такая операция приведет нас к дроби, знаменатель которой есть разность радикалов.

Заметим, что первое слагаемое в первой части тождества есть число большее, чем второе, поэтому можно возвести обе части в квадрат:

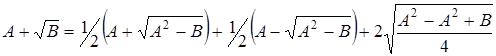
0=0, ч.т.д.