Реферат: Тождественные преобразования выражений и методика обучения учащихся их выполнению
л) Решить уравнение ![]() .
.
Эти задания направлены на возможно более полное использование и учет специфики именно данного тождества, предполагают сформированность навыков использования изучаемого тождества для разности квадратов. Цель – углубить понимание тождества за счет рассмотрения разнообразных приложений его в различных ситуациях, в сочетании с использованием материала, относящегося к другим темам курса математики.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
или ![]() .
.
Особенности циклов заданий, связанных с тождествами для элементарных функций:
1) они изучаются на базе функционального материала;
2) появляются позже тождества первой группы и изучаются с использованием уже сформированных навыков проведения тождественных преобразований.
В первую группу заданий цикла должны войти задания на установление связи этих новых числовых областей с исходной областью рациональных чисел.
Пример.
Вычислить:
![]()
![]()
![]() ;
;
![]()
![]()
![]() ;
;
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
Цель таких заданий – освоение особенностей записей, включающих символы новых операций и функций, и в развитии навыков математической речи.
Значительная часть использования тождественных преобразований, связанных с элементарными функциями, приходится на решение иррациональных и транцендетных уравнений. Последовательность шагов:
а) найти функцию φ, для которой данное уравнение f(x)=0 представимо в виде:
F(φ(x))=0;
б) произвести подстановку y=φ(x) и решить уравнение
F(y)=0;
в) решить каждое из уравнений φ(x)=yk , где yk -множество корней уравнения F(y)=0.
При использовании описанного способа зачастую шаг б) выполняется в неявном виде, без введения обозначения для φ(x). Кроме того, ученики зачастую предпочитают из различных путей, ведущих к нахождению ответа, выбирать тот, который быстрее и проще приводит к алгебраическому уравнению.
Пример. Решить уравнение 4x -3*2=0.
1)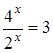 ;
;
2)(22 )x -3*2x =0 (шаг а)
(2x )2 -3*2x =0; 2x (2x -3)=0; 2x -3=0. (шаг б)
Пример. Решить уравнение:
а) 22x -3*2x +2=0;
б) 22x -3*2x -4=0;