Радиоэлектроника / Реферат: Цифровая обработка сигналов

Реферат: Цифровая обработка сигналов

то после перехода к дискретной переменной пара преобразований Фурье принимает вид

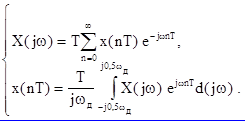
Здесь применяются формулы одностороннего преобразования Фурье, так как начало отсчета совмещается с началом действия дискретного сигнала.

Формулы Фурье для дискретных сигналов применяются в нормированном виде, поэтому после замены X(nT) ® X(nT) / T преобразование Фурье принимает окончательный вид

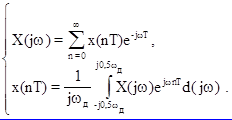(1.5)

Формулы Лапласа для дискретных сигналов получаются на основании (1.5) после обобщения частоты на всю плоскость комплексного переменного, то есть jw® P = d + jw

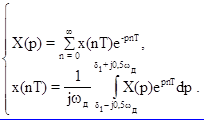(1.6)

1.4. Z - преобразование.

Эффективность частотного анализа дискретных сигналов существенно возрастает, если заменить преобразование Лапласа Z - преобразованием. В этом случае изображение сигнала X(p), которое представляет собой трансцендентную функцию переменной P = d + jw, заменяется Z - изображением сигнала X(Z), которое является рациональной функцией переменной Z = x + jy.

Формулы Z - преобразования получаются из формулы Лапласа (1.6) заменой переменных

e^pT = Z . (1.7)

Подстановка (1.7) и ее производной

dZ / dp = Te^pT

в (1.6) приводит к формулам прямого и обратного Z - преобразования

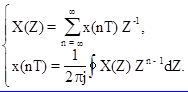(1.8)

Точки на мнимой оси комплексного переменного p = d +jw, то есть точки p = jw, определяют реально частотные характеристики сигнала. Мнимой оси соответствует на плоскости Z единичная окружность, так как в этом случае согласно (1.7)

Z = e^j ^w ^T = (1.9)

Поэтому непрерывному росту переменной на мнимой оси плоскости p = d + jw, соответствует многократный обход единичной окружности на плоскости z = x + jy (Рис. 1.4). Этим фактом объясняется, в частности, то обстоятельство, что интегрирование в формуле обратного z - преобразования (1.8) осуществляется вдоль единичной окружности плоскости z взамен интегрирования вдоль прямой параллельной мнимой плоскости p.

Учитывая вышеизложенное и формулы (1.7), (1.9) можно утверждать, что левая полуплоскость переменного p = d + jw отображается на плоскость единичного круга переменного z = x + jy, правая полуплоскость - на плоскость z за пределами единичного круга.

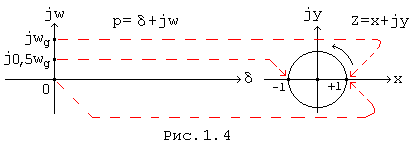
Подстановка (1.9) в z - изображение сигнала приводит к спектру этого сигнала, подстановка (1.7) дает изображение по Лапласу.

Пример. Определить спектр и построить графики модуля и аргумента спектральной плотности сигнала x(nT) = {a ; b} (Рис. 1.5, а).

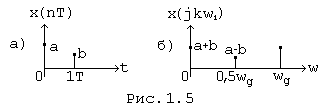
Решение.

Z - изображение сигнала согласно (1.8)

X(Z) =x(nT) Z^-n = x(0T) Z^-0 + x(1T) Z^-1 = a + bZ^-1

Отсюда подстановкой (1.9) определяем спектр сигнала

X(jw) = a + be^-j ^w ^T .

Графики модуля и аргумента спектральной плотности приведены на рисунке 1.6, а, б на интервале частот [0 ; w_д ].

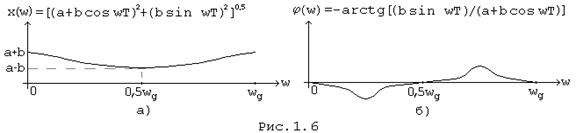
Вне интервала частот [0 ; w_д ] частотные зависимости повторяются с периодом w_д .

1.5 Основные теоремы Z - преобразования.

Перечислим без доказательства теоремы z - преобразования, которые потребуются в последующих разделах.

1. Теорема линейности.

Если x(nT) = ax₁ (nT) + bx₂ (nT) ,

то X(Z) = a X₁ (Z) + bX₂ (Z).

2. Теорема запаздывания.

Если x(nT) = x₁ (nT - QT) ,

то X(Z) = X₁ (Z) Z^-Q .

3. Теорема о свертке сигналов.

Если X(nT) = x₁ (kT) x₂ (nT - kT) ,

то X(Z) = X₁ (Z) X₂ (Z).

4. Теорема об умножении сигналов.

Если x(nT) = x₁ (nT) x₂ (nT) ,

то X(Z) = X₁ (V) X₂ () V^-1 dV,

где V, Z - переменные на плоскости Z.

5. Теорема энергий (равенство Парсеваля).

x² (nT) =X(Z) X(Z^-1 ) Z^-1 dZ.

Z - преобразование дискретных сигналов имеет значение равное значению преобразования Лапласа непрерывных сигналов.

1.6. Дискретное преобразование Фурье.

Если сигнал ограничен во времени значением t_u , а его спектр - частотой w_в , то он полностью характеризуется конечным числом отсчетов N как во временной, так и в частотной областях (Рис. 1.7, а, б) :

N = t_u /T - во временной области, где T = 1/f_д ,

N = f_д /f₁ - в частотной области, где f₁ = 1/t_u .

Дискретному сигналу соответствует периодический спектр, дискретному спектру будет соответствовать периодический сигнал. В этом случае отсчеты X(nT) = {X₀ ; X₁ ; … X_N-1 } являются коэффициентами ряда Фурье периодической последовательности X(jkw₁ ), период, который равен w_д . Соответственно, отчеты X(jkw₁ ) = {X₀ ; X₁ ; … X_N-1 } являются коэффициентами ряда Фурье периодической последовательности X(nT), период, который равен t_u .

Связь отсчетов сигнала и спектра устанавливается формулами дискретного преобразования Фурье (ДПФ). Формулы ДПФ следуют из формул Фурье для дискретных сигналов (1.5), если непрерывную переменную w заменить дискретной переменной kw₁ , то есть

w® kw₁ , dw®w₁ .

После замены переменной в (1.5) получим

X(jkw₁ ) = x(nT),