Реферат: Цифровая обработка сигналов

n=0 : y(0T) = h(0T)x(0T) = 0;

n=1 : y(1T) = h(0T)x(1T) + h(1T) x(0T) = 0,4;

n=2 : y(2T)= h(0T)x(2T) + h(1T) x(1T) + h(2T) x(0T) = 0,168;

Таким образом y(nT) = { 0; 0,4; 0,168; ... }.

В технических системах вместо линейной свертки (2.12) чаще применяется круговая или циклическая свертка .

2.6 Круговая свёртка .

Реальным сигналам соответствуют числовые последовательности конечной длины. Конечную числовую последовательность можно продолжить по оси времени путём периодического повторения и получить периодическую числовую последовательность. Периодической числовой последовательности соответствует спектр в виде периодической числовой последовательности. Обе последовательности имеют одинаковый период N и связаны формулами ДПФ.

Замена реальных последовательностей периодическими позволяет повысить эффективность использования вычислительной техники применительно к дискретным сигналам (скоростная свёртка, БПФ и др. )

Свёртка периодических последовательностей называется круговой и определяется на интервале равном одному периоду.

y(nT) =x(kT)Чh(nT - kT), (2.13)

Линейная и круговая свёртки дают одинаковый результат, если соответствующим образом выбрать в круговой свёртке размер исходных последовательностей. Дело в том, что свёртка конечных последовательностей приводит к последовательности, размер которой N превышает длину каждой из исходных последовательностей и, по определению, равен

N = N₁ + N₂ - 1, (2.14)

где N₁ - длина последовательности x(nT),

N₂ - длина последовательности h(nT).

Поэтому замена исходной последовательности на периодическую выполняется с таким расчётом, чтобы длина периода получилась равной N, добавляя с этой целью нули в качестве недостающих элементов.

Пример.

Вычислить круговую свёртку по данным примера в параграфе 2.4.

Решение.

Здесь, пренебрегая малыми значениями отсчётов представим импульсную реакцию в виде конечной числовой последовательности h(nT) ={0; 0,4 ; -0,032}.

Отсюда, поскольку x(nT) = {1,0; 0,5}, с учётом (2.14)

N₁ = 2,N₂ = 3,N = 4.

Следовательно исходные числовые последовательности запишутся так

x(nT) = {1,0; 0,5; 0; 0}, h(nT) ={0; 0,4; -0,032; 0}.

Отсюда, применяя (2.13), получаем

n=0: y(0T) = x(0T)h(0T) + x(1T)h(-1T) + x(2T)h(-2T) + x(3T)h(-3T) = 0;

n=1: y(1T) = x(0T)h(1T) + x(1T)h(0T) + x(2T)h(-1T) + x(3T)h(-2T) = 0,4;

n=2: y(0T) = x(0T)h(2T) + x(1T)h(1T) + x(2T)h(0T) + x(3T)h(-1T) = 0,168;

n=3: y(0T) = x(0T)h(3T) + x(1T)h(2T) + x(2T)h(1T) + x(3T)h(0T) = -0,016;

Следовательно y(nT)= {0; 0,4; 0,168; -0,016}, что совпадает с расчётами по линейной свёртке в примере параграфа 2.4.

Графики периодических числовых последовательностей x(nT), h(nT), y(nT) приведены на рис.(2.7).

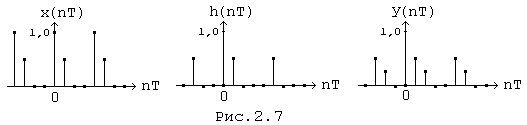
К периодическим числовым последовательностям, полученным изложенным выше способом, можно применить ДПФ, перемножить результаты и после выполнения обратного ДПФ получить последовательность y(nT), совпадающую с результатами расчётов по круговой свёртке.

2.7. Энергия дискретного сигнала.

Корреляция и энергетический спектр.

В качестве энергии дискретного сигнала принята мера

W_x =x² (nT), (2.15)

соответственно в частотной области, согласно равенству Парсеваля,

W_x =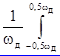X² (w)dw =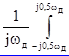X(jw)X^* (jw)d(jw), (2.16)

где X(jw) = X(w)e^{j j ( w )} - спектр сигнала x(nT),

X^* (jw) = X(w)e^{-j j ( w )} - спектр x(-nT) в соответствии с теоремой о спектре инверсного сигнала,

X² (w) = X(jw)ЧX^* (jw) = S_x (jw) - энергетический спектр сигнала x(nT).

На рис.(2.8) показан в качестве примера сигнал x(nT) и его инверсная копия x(-nT) для некоторого частного случая

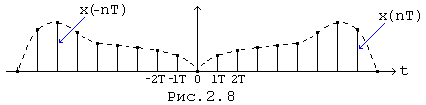
Энергетический спектр выражает среднюю мощность сигнала x(nT), приходящуюся на узкую полосу частот в окрестности переменной w.

Во временной области энергетическому спектру соответствует свертка инверных сигналов, что определяет корреляционную функцию S_x (nT) сигнала x(nT).

. (2.17)

Согласно (2.17) и (2.15) корреляционная функция в точке n = 0 равна энергии сигнала, т. е.

(2.18)