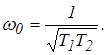Реферат: Устойчивость линейных систем автоматического управления

Годограф устойчивой системы имеет вид (рис. 3a).

Пример 5. Допустим, задан характеристический полином системы

Годограф устойчивой системы имеет вид (рис. 3б).

Пример 6. Допустим, задан характеристический полином системы

Годограф устойчивой системы имеет вид (рис. 3в).

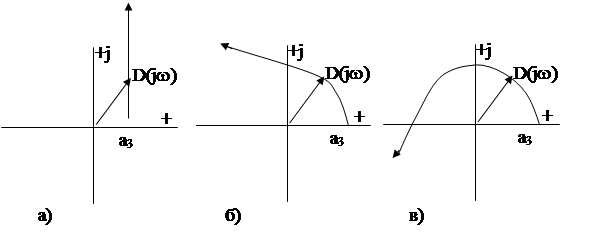Рис. 3

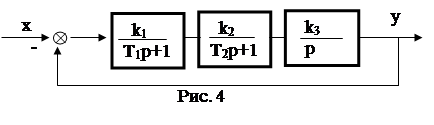
Пример. Для заданной системы (рис. 4) определить условие устойчивости, частоту собственных колебаний системы и критический коэффициент усиления, т.е. коэффициент усиления, при котором система находится на границе устойчивости.

Определить устойчивость при T₁ = T₂ = 1 c и k_v = 1 c^-1 .

Решение:

1. Определяем передаточную функцию разомкнутой системы

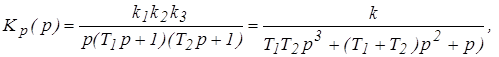
где

2. Определяем передаточную функцию замкнутой системы

3. Запишем характеристическое уравнение

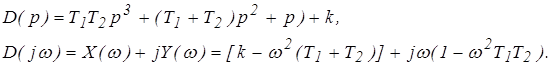
4. Определим частоту собственных колебаний системы и критический коэффициент усиления из условия границы устойчивости

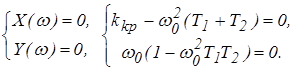
Откуда частота собственных колебаний системы равна:

Критический коэффициент усиления равен:

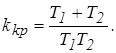
5. Определим устойчивость при T1 = T2 = 1 c и kv = 1 c-1.

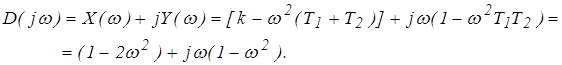
5. Строим характеристическую кривую(рис. 5) по данным, приведенным в таблице 1.

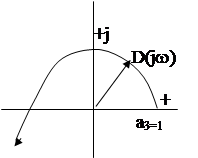Таблица 1

w	0		1	¥
X(w)	1	0	-1	-¥
Рис. 5 Y(w)	0		0	-¥

В соответствии с критерием Михайлова, рассматриваемая система является устойчивой.

4. Частотный критерий устойчивости Найквиста