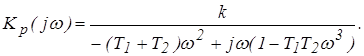Реферат: Устойчивость линейных систем автоматического управления

Рассмотрим функцию, которая связывает характеристики разомкнутых и замкнутых систем

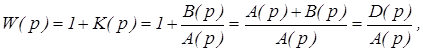(6)

где D(p) – характеристический полином замкнутой системы;

A(p) – характеристический полином разомкнутой системы.

При этом степени полиномов A(p) и D(p) одинаковы исходя из условия физической реализуемости системы.

В соответствии со следствием из принципа аргумента

(7)

Рассмотрим разные случаи.

Система, устойчивая в разомкнутом состоянии.

Так как разомкнутая система устойчива, то она не содержит корней в правой полуплоскости (т.е. m = 0), для того чтобы и замкнутая система была устойчива, должно выполняться условие:

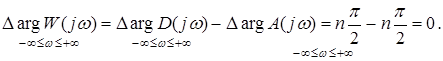(8)

Графически это обозначает, что годограф вектора W (jw) не охватывает начала координат, а вектора K (jw) – точку с координатами (-1, j0), как показано на рис. 6. Точка с координатами (-1, j0) называется критической.

Рис. 6.

Система, неустойчивая в разомкнутом состоянии.

Так как разомкнутая система неустойчива, то она содержит m корней в правой полуплоскости, для того, чтобы замкнутая система была устойчивой, должно выполняться условие

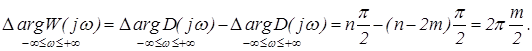(9)

Графически это обозначает, что годограф вектора K (jw) охватывает точку с координатами (-1, j0) m/2 – раз.

Формулировка критерия Найквиста: Замкнутая система автоматического управления устойчива, если амплитудно-фазовая частотная характеристика разомкнутой, неустойчивой системы, имеющей m корней в правой полуплоскости, охватывает точку с координатами (–1, j0) m/2-раз.

Иногда по графику трудно определить охватывает ли АФХ критическую точку. В этом случае можно использовать правило переходов. Переходами называются точки пересечения АФХ отрезка оси (-¥.. – 1). Знак перехода определяется по следующему правилу: если фаза убывает – переход отрицательный.

Формулировка критерия Найквиста: Замкнутая система автома-тического управления устойчива, если разность положительных и отрицательных переходов равна m/2, где m – количество корней в правой полуплоскости разомкнутой неустойчивой системы, т.е.

S - S= m/2.

(10)

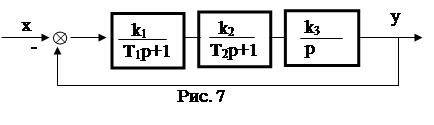
Пример 8. Для заданной системы (рис. 7) определить условие устойчивости и критический коэффициент усиления.

Определить устойчивость при T₁ = T₂ = 1 c и k_v = 1 c^-1 .

Решение:

1. Определяем передаточную функцию разомкнутой системы

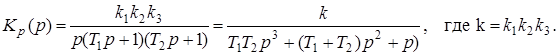
2. Строим АФХ разомкнутой системы