Реферат: Устойчивость линейных систем автоматического управления

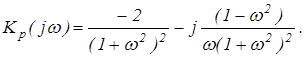
Расчетные данные приведены в таблице 2, а график АФХ на рис. 8.

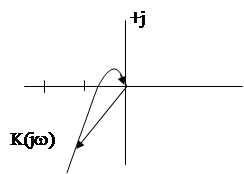Таблица 2

w	0	1	¥
P(w)	-2	-1/2	0
Q(w)	-¥	-2 -1 w=¥+ 0	0

Рис.8

Как видно из рисунка (8) и таблицы 2, АФХ разомкнутой системы не охватывает критическую точку, следовательно, замкнутая система, при заданной структуре и параметрах, устойчива.

Определим критический коэффициент усиления из условия:

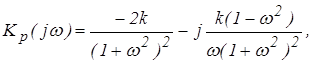
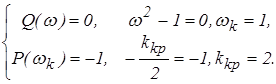
5. Определение областей устойчивости

Устойчивость систем зависит от структуры и параметров системы. При расчете систем автоматического управления возникает задача опреде-ления диапазона изменения варьируемых параметров системы, при кото-рых она устойчива.

Область устойчивости – это совокупность значений параметров системы, при которых она устойчива.

Коэффициенты характеристического уравнения являются функциями от параметров системы, и они определяют расположение корней в комплексной плоскости, при изменении параметров корни перемещаются в комплексной плоскости и система может стать не устойчивой.

Для определения областей устойчивости можно использовать различные методы, наиболее часто используют метод D – разбиения. D-разбиение может быть выполнено по одному и более параметрам.

Рассмотрим алгоритм определения областей устойчивости с помощью метода D – разбиения по одному параметру на конкретных примерах.

Пример 9. Определить область возможных значений параметра «к», при которых заданная система (рис. 9) устойчива

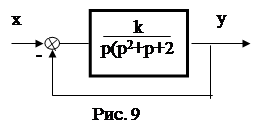Порядок определения областей устойчивости

1. Определяем передаточную функцию замкнутой системы

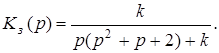
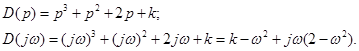
2. Определяем характеристический полином

3. Разрешим уравнение относительно параметра – к

4. Строим кривую D – разбиения (см. таблицу 3 и рис. 10)

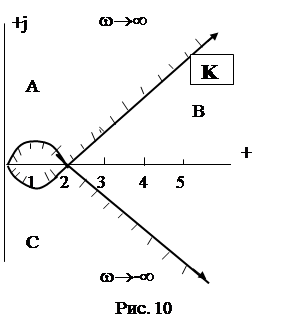Таблица 3

w	0	1	Ö2	2	¥
X(w)	0	1	2	4	¥
Y(w)	0	-1	0	4	¥

5.Определяем область устой-чивости по правилу штрихов-ки (устойчивая область распо-ложена слева при j w ® ¥ и справа при j w ® - ¥ ). Претенде-нтом на устойчивостьявляется область D.

D

Так как параметр является вещественной положительной величиной, то областью устойчивости являются значения параметра – к, расположенные на вещественной положительной оси, т.е.] 0, 2 [, что может быть провере-но по критерию Гурвица.

Литература

1. Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986.

2. Брюханов В.Н. и др. Теория автоматического управления. – М: Высшая школа, 2000.

3. Егупов Н.Д., Пупков К.А., Баркин А.И. Синтез регуляторов систем автоматического управления. МГТУ им. Н.Э. Баумана, 2004.

4. Ким Д.П., Дмитриева Н.Д. Сборник задач по теории автоматического управления. Линейные системы. ФИЗМАТЛИТ, 2007. – 168 с.