Реферат: Взаимосвязи экономических перемененых
Пояснение ![]()
![]()
5). Модель яв-ся линейной отн-но ее парам-ов βо β1.
Теорема Гаусса-Маркова.
Основ-ся на предпосылках МНК.
Если все 5 предпос-к вып-ся, то оценки коэф-в, получ-е с помощью МНК облад-т след сво-вами:
А). Оценки яв-ся несмещенными, т.е.
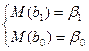
Б). Оценки яв-ся состоятельными, т.к. дисп-ии их с ростом объема выборки стрем-ся к 0.
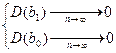
Т.е. ↑ объема выборки приводит к устойчивости оценок коэф-в ур-ия. Сч-ся, что объем выборки д удовл-ть соот-ию n>3m-1, где m-кол-во объясняющих переем-х.
В). Оценки эфф-ны, т.е. они имеют наименьшую дисп-ию разброса отн-но теорет-х вел-н по срав-ию с такими же оценками полученных с примен-м и люб др методов расчета.
В англоязыч науч лит-ре эти оценки получ-ли название BLUE (голубые оценки) по первыем буквам (наилуч лин состоят эффект). Если наруш-ся предпосылки 2 и 3, то дисп-ии откл-ий не пост-ны, случ откл-ия связаны др с др и коэф-ты теряют св-ва несмещен-ти и эффек-ти.
При этос б сделаны след предположения:
1). Объясняющ перем-ые не яв-ся случ.
2). Случ вел-ны εi имеют норм распр-ие с пар-ми 0 и ε²
εi²~N(0;σ²)
Число набл-ий n>3m-1 сущ-но > числа объясняющ перем-х. Отсут-т ошибки специф-ии. М/у объясняющ перем-ми в случае m≥2 отсут-т зав-т (мультикол-ть).
Анализ точности определения оценок коэффициентов регрессии.
Изв-но, что мат ожидания расчет коэф-в совпадают с их теоретич вел-ми
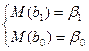
При этом чем < откл-ие оценок от этих теоретич вел-н, тем надежнее построенное ур-ие.
Покажем, что дисп-ии оценок D(b1) и D(bo) непоср-но связаны с дисп-ей случ откл-ий в теоретич модели D(εi)=D(εj)=σ²=consti≠j.
Для этого запишем вел-ну b
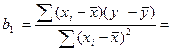
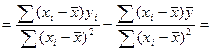
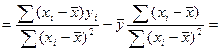
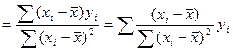
Обозначим за ![]()
=∑Сiyi
Аналог-но преобр-м знач-е для bo.