Реферат: Взаимосвязи экономических перемененых

=> к-т b1 имеет норм распр-ие с пар-ми β1, D(d1).

Поэтому t стат-ка для коэф-та подчинена распр-ию Стьюдента с доверит-й вер-тью γ=1-α, что соот-т утвер-ию

Тогда мы м записать, что вер-ть

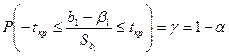
Преобр-м выраж-ие, стоящее в скобках

-tкрSb1≤b1-β1≤tкрSb1

-b1-tкрSb1≤-β1≤tкрSb1-b1

-b1-tкрSb1≤β1≤b1+tкрSb1

Получ соот-ие дает доверит-й инт-л, кот-ый с надеж-тью 1-α покрывает теорет коэф-т β1.

Доверительные интервалы для зависимой переменной.

Одной из осн-х задач эконометр анализа яв-ся прогнозир-ие знач-ий завис перем-ой при опр-ых знач-ях Хпр объясн-й перем-ой.

Здесь возм-н двоякий подход. Либо предсказ-ся усл-ое мат ожидание объясн-й перем-ой при нек-ой объясн-й перем-ой Хпр. М(У/х=Хпр). Либо прогноз-ся нек-ое конкр значение завис перем-ой при извест-м значении объясн-й перем-ой. Тогда гов-т о предсказании конкр вел-ны

1). Предсказание ср значения.

Предпол-м, что мы построили нек эмпир значение парной регр-ии ỹi=b0+b1xi, на основе кот-го хотим предсказать ср вел-ну завис перем-й у при х=Хпр. В данном случае рассчит-ое по урав-ию вел-на ỹпр=b0+b1xпр яв-ся только оценкой для искомого мат ожидания.

Встает вопрос насколько м эта оценка откл-ся от ср мат ожидания для того, чтобы ей м.б. доверять с надеж-тью γ=1-α.

Чтобы построить доверит инт-л, покажем, что случ вел-на ỹпр имеет норм распр-ие с нек-ми конкр переем-ми.

Мы знаем, что ỹпр=b0+b1xпр. Подставим в это ур-ие знач-ие для bo и b1, найденное в виде лин комбинаций выборочных вел-н объясн-й перем-й yi.

Т.е. мы пок-ли, что расчет вел-на яв-ся лин комб-ей нормально распред-й случ вел-ны yi=> она дейст-но имеет норм распред-ие и мы м рассч-ть пар-ры этого распред-ия М(Ỹпр) и D(Ỹпр).

М(Ỹпр)=M(bo+b1Xпр)= М(bo)+XпрM(b1) = βo+Xпрβ1

D(Ỹпр)=D(bo+b1Xпр) =

Т.к. bo вычисл-ся ч/з значение для b1, то они м/у собой зависят и поэтому

= D(bo)+X²прM(b1)=2cov(bo,b1Xпр)***=

Рас-м вел-ну ковариации.

Заменим вел-ну bo ч/з правило ее вычисления из эмпир ур-ия регр-ии, аналог-но поступим со знач-ем βо, записав его знач-ие ч/з теорет ур-ие регр-ии.

Тогда получаем