Реферат: Взаимосвязи экономических перемененых

Обозначим

=∑diyi

Причем Ci и di –нек-ые const рассчит-е по выборке, что очевидно из их обозначений.

Оценим теперь вел-ну дисп-ий для коэф-та b1

D(b1)=D(∑Ciyi)=

И т.к. мы знаем значение для дисп-ии разброса случ откл-ий, то м записать

=σ²∑Сi²=

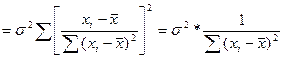
Т.о. мы нали знач-ие дисп-ии на основе дисп-ии теоретич откл-ия ε.

Аналог-но для bo.

Мы м получить, что она равна

D(bo)=D(b1)x²

Т.о. дисп-ия разброса коэф-та прямопропорц-на дисп-ии случ откл-ий => чем > фак-р случ-ти, тем менее точными б оценки и чем > число набл-ий в выборке, тем меньше б эти вел-ны разбросаны.

Кроме того дисп-ии обратнопропорц-ны выбороч дисп-ии объясняющ перем-й S²x, т.е. чем шире область изм-ий объясняющ перем-й, тем точнее б оценки. Но в силу того, что дисп-ии случ теоретич откл-ий σ² нам неиз-ны, мы б их заменять несмещен-й дисп-ей расчет случ откл-ий.

,

где m- число объясняющ переем-х. Для парной регр-ии .

Тогда стандарт откл-ия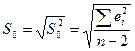

Наз-ся стандартной ошибкой в случ откл-ии. И для того, чтобы рассч-ть дисп-ию разброса коэф-в эмпир-го ур-ия регр-ии, мы б исп-ть формулы

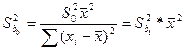
Проверка гипотез относ-но коэф-ов лин ур-ия регр-и.

Эмпир ур-ия регр-ии строятся на основе конеч выборки, извлеч-й из генер сов-ти случ образом, поэтому как б показано коэф-ты ур-ия яв-ся случ вел-нами.

При проведении эк анализа перед иссл-лями оч часто возн-т необ-ть сравнить расчет коэф-ты bo и b1 с нек-ми теоретич коэф-ми βо и β1.

Это срав-ие осущ-ся по схеме проверки гипотез. Предпол-м, провер-ся гипотеза Но:, состоящая в том, что эти вел-ны совпадают.

Но:=b1=β1. Тогда с ней конкурир-ая гипотеза Н1: не совпадает. Как изв-но из тер.вера для проверки таких гипотез рассч-ся t стат-ка Стьюдента, кот-ая при справед-ти гипотезы но имеет распред-ие Стьюдента с числом степеней свободы с парной регр-ей

tb1= (b1-β1)/Sb1