Реферат: Застосування частинних похідних

1. Дотична площина та нормаль до поверхні. Геометричний зміст диференціала функції двох змінних

Нехай задано поверхню

. (1)

Точка належить цій поверхні і функція диференційована в точці , причому не всі частинні похідні в точці дорівнюють нулю, тобто

.

Розглянемо довільну криву, яка проходить через точку , лежить на поверхні (1) і задається рівнянням

де точці відповідає параметр .

Оскільки крива лежить на поверхні, то координати її точок задовольняють рівняння (1):

. (2)

Диференціюючи рівність (2), маємо:

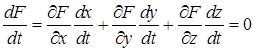. (3)

Ця рівність показує, що вектори (рис. 1)

ортогональні, причому другий з них є напрямним вектором дотичної до кривої у точці .

Крім того, з рівності (3) випливає, що дотичні до всіх кривих, які проходять через точку і лежать на поверхні (1), ортогональні до одного й того самого вектора . Тоді всі ці дотичні лежать в одній і тій самій площині, яка називається дотичною площиною до поверхні в точці .

Знайдемо рівняння дотичної площини. Оскільки ця площина проходить через точку перпендикулярно до вектора , то її рівняння має вигляд.

.(4)

Нормаллю до поверхні в точці називають пряму, що проходить через точку перпендикулярно до дотичної площини в цій точці.

Оскільки нормаль проходить через точку і має напрямний вектор , то канонічні рівняння нормалі мають такий вигляд:

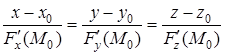. (5)

Якщо рівняння поверхні задано в явній формі, то, поклавши, отримаємо

,

тоді рівняння (4) і (5) наберуть вигляду:

;(6)

.(7)

Рисунок 1 – Дотична площина та нормаль до поверхні

--> ЧИТАТЬ ПОЛНОСТЬЮ <--