Реферат: Застосування частинних похідних

5. Нехай і, тоді і

.

При досить малих кутах знак величини збігається зі знаком , тому знак величини залежатиме від знака множника. Але знак величини змінюється при і, бо . Отже, в достатньо малому околі точки знак не збігається, тобто функція в цій точці екстремуму не має.

Зауваження . З доведення теореми 2 випливають так звані другі достатні умови екстремуму : функція має мінімум у стаціонарній точці, якщо диференціал другого порядку в цій точці , і максимум – якщо .

Можна довести, що другі достатні умови екстремуму справедливі для функцій довільного числа змінних.

На основі теорем 1 і 2 отримаємо правило дослідження диференційовних функцій двох змінних на екстремум. Щоб знайти екстремум диференційовної функції, необхідно:

1) знайти стаціонарні точки функції із системи рівнянь:

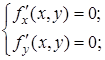
2) у кожній стаціонарній точці обчислити вираз

;

якщо , то – точка екстремуму функції, причому точка максимуму при і мінімуму при; якщо, то точка не є точкою екстремуму функції;

3) обчислити значення функції у точках максимуму та мінімуму.

Якщо, то ніякого висновку про характер стаціонарної точки зробити не можна і потрібне додаткове дослідження.

5. Найбільше та найменше значення функції

диференціал функція дотична нормаль екстремум

Відомо, що функція, задана і неперервна в замкненій та обмеженій області, досягає в цій області найбільшого і найменшого значень. У внутрішніх точках області диференційовна функція може набувати цих значень лише в точках локального екстремуму. Тому потрібно знайти всі стаціонарні точки функції, які належать області,розв'язавши систему рівнянь, і обчислити значення функції в цих точках. Потім потрібно дослідити функцію на екстремум на межі області.Використовуючи рівняння межі, цю задачу зводять до знаходження абсолютного екстремуму функції однієї змінної [8]. Серед здобутих таким чином значень функції всередині і на межі області вибирають найбільше і найменше значення.

Зазначимо, що загального методу знаходження найбільшого та найменшого значень для довільної неперервної функції в замкненій та обмеженій області немає.