Реферат: Застосування частинних похідних

Справді, з формули (10) випливає, що похідна за напрямом досягає максимального значення (11), якщо , тобто якщо напрям вектора збігається з напрямом градієнта.

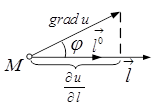
Рисунок 4 – Зв'язок між градієнтом і похідною за напрямом

Таким чином, швидкість зростання скалярного поля в довільній точці є максимальною у напрямі градієнта .Зрозуміло, що у напрямі, протилежному до напряму градієнта, поле найшвидше зменшуватиметься.

2. Похідна за напрямом вектора, перпендикулярного до градієнта, дорівнює нулю . Інакше кажучи, швидкість зміни поля у напрямі, перпендикулярному до градієнта, дорівнює нулю, тобто скалярне поле залишається сталим.

Справді, за формулою (10), якщо.

Вектор-градієнт у кожній точці поля перпендикулярний до поверхні рівня, яка проходить через цю точку .Це твердження випливає з того, що напрямний вектор нормалі до поверхні рівня, яка проходить через точку має координати (п. 1)

.

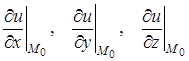4. Справедливі рівності :

.

Доведення

Доведемо, наприклад, третю рівність. Маємо:

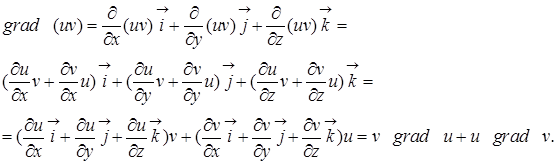
Решта рівностей доводяться аналогічно.

3. Формула Тейлора для функції двох змінних

Якщо функція однієї змінної має на відрізку неперервні похідні до -го порядку включно, то справджується формула Тейлора:

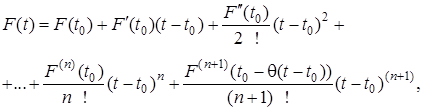(12)

.

Нехай ,

тоді, тому формулу (12) можна записати у вигляді

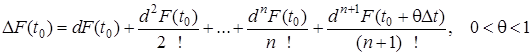.(13)

В аналогічному вигляді формулу Тейлора можна отримати і для функції багатьох змінних. Розглянемо функцію двох змінних.

Нехай функція в області має неперервні частинні похідні до -го порядку включно. Візьмемо дві точки та такі, щоб відрізок належав області.

Введемо нову змінну :

, , .(14)