Реферат: Застосування частинних похідних

Доведення

Нехай – точка екстремуму. Тоді функція буде функцією однієї змінної. Ця функція має екстремум у точці ц, тому її похідна дорівнює нулю або не існує.

Аналогічно, розглянувши функцію отримаємо, що

дорівнює нулю або не існує.

Подібна теорема справедлива для функції n змінних. Точку, в якій частинні похідні першого порядку функції дорівнюють нулю, тобто, називають стаціонарною точкою функції .

Стаціонарні точки та точки, в яких частинні похідні не існують, називаються критичними точками .

Таким чином, якщо функція в будь-якій точці досягає екстремуму, то це може статися лише в критичній точці. Проте не всяка критична точка є точкою екстремуму, тобто теорема 1 встановлює лише необхідні, але не достатні умови екстремуму. Наприклад, частинні похідні функції дорівнюють нулю в точці. Але ця функція у вказаній точці екстремуму не має, тому що в досить малому околі точки вона набуває як додатних (при), так і від'ємних (при) значень.

Слід зазначити, що в задачах з практичним змістом, як правило, відомо, що функція має екстремум. Якщо така функція має лише одну критичну точку, то ця точка і буде точкою екстремуму.

Теорема 2 (достатні умови екстремуму). Нехай у стаціонарній точці і деякому її околі функція має неперервні частинні похідні другого порядку . Якщо

,

то функція має в точці екстремум, причому максимум при і мінімум при . Якщо , то в точці функція екстремуму не має .

Доведення

Запишемо формулу Тейлора (23) для функції в околі стаціонарної точки.Враховуючи, що, отримаємо:

У випадку мінімуму для довільних достатньо малих значень та права частина цієї рівності має бути додатною, а у випадку максимуму – від'ємною.

Внаслідок неперервності других частинних похідних для цього достатньо, щоб диференціал другого порядку в точці

зберігав знак для малих значень та.

Введемо такі позначення, , , тоді

.

Нехай – кут між відрізком , де – точка з координатами і віссю; тоді., тому при маємо

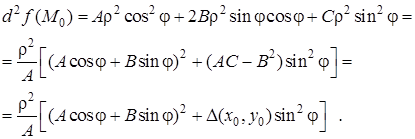
Розглянемо тепер п’ять можливих випадків.

1. Нехай і, тоді , тому при досить малих значеннях приріст, тобто функція має в точці максимум.

2. Аналогічно доводимо, що коли і, то функція має в точці мінімум.

Нехай і. Якщо з точки рухатися вздовж променя

, то. Якщо взяти таким, щоб або , то

.

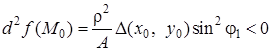Отже, при малих значеннях приріст в околі точки не зберігає знак, тому ця точка не є точкою екстремуму функції.