Реферат: Застосування частинних похідних

,

де – нескінченно малі функції при.

Оскільки

то

.

Перейшовши до границі при, отримаємо формулу для обчислення похідної за напрямом

.(8)

З формули (З.8) випливає, що частинні похідні є окремими випадками похідної за напрямом. Дійсно, якщо збігається з одним із ортів, або ,то похідна за напрямом збігається з відповідною частинною похідною. Наприклад, якщо, то, тому

.

Подібно до того як частинні похідні характеризують швидкість зміни функції в напрямі осей координат, так і похідна показує швидкість зміни скалярного поля в точці за напрямом вектора.

Абсолютна величина похідної відповідає значенню швидкості, а знак похідної визначає характер зміни функції в напрямі (зростання чи спадання).

Очевидно, що похідна за напрямом, який протилежний напряму, дорівнює похідній за напрямом, взятій з протилежним знаком.

Справді, при зміні напряму на протилежний кути зміняться на , тому

.

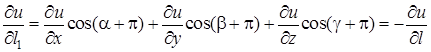Фізичний зміст цього результату такий: зміна напряму на протилежний не впливає на значення швидкості зміни поля, а тільки на характер зміни поля. Якщо, наприклад, в напрямі поле зростає, то в напрямі воно спадає, і навпаки.

Якщо поле плоске, тобто задається функцією то напрям вектора цілком визначається кутом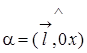. Тому, поклавши у формулі (8) та, отримаємо

.

Вектор, координатами якого є значення частинних похідних функції в точці називають градієнтом функції в цій точці і позначають.Отже,

. (9)

Зв'язок між градієнтом і похідною в даній точці за довільним напрямом показує така теорема.

Теорема. Похідна функції у точці за напрямом вектора дорівнює проекції градієнта функції в цій точці на вектор , тобто

.(10)

Доведення

Нехай – кут між градієнтом (9) і одиничним вектором (рис. 4), тоді з властивостей скалярного добутку [1] отримаємо

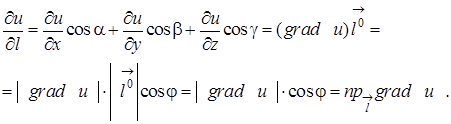
Зазначимо деякі властивості градієнта .

1. Похідна в даній точці за напрямом вектора має найбільше

значення, якщо напрям вектора збігається з напрямом градієнта, причому