Шпаргалка: Лекции по статистике
1 квартиль или нижний отделяет четверть ранжированной совокупности снизу и вычисляется по формуле:
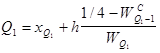(для интервального)
Медиану можно рассматривать как второй квартиль.
Верхний квартиль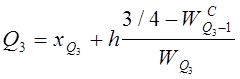 
Мода.
Мода - наиболее часто встречающееся в совокупности значение признака. Для дискретного вариационного ряда мода определяется по частотам вариант и соответствует варианте с максимальной частотой. При определении моды обычно применяют следующие соглашения:
1. если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды.
2. если две соседних варианты имеют одинаковую доминирующую частоту, что мода вычисляется как среднее арифметическое этих вариант.
3. если две не соседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным.
4. если таких вариант более двух, то ряд - полимодальный.
В случае интервального вариационного ряда с равными интервалами модальный интервал определяется по наибольшей частоте, а при неравных интервалах - по наибольшей плотности.
При равных интервалах мода внутри модального интервала может определяться по следующей формуле:
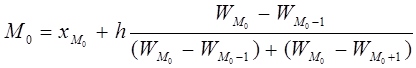
Данная формула получена исходя из допущения, что в модальном и двух соседних интервалах кривая распределения представляет собой параболу второго порядка. Тогда мода находится как вершина параболы. Для графического определения моды используют 3 соседних столбца гистограммы (самый высокий и 2 прилегающих к нему).
При вычислении моды в формуле можно использовать не только относительные, но и другие частоты.
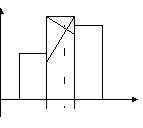
пример.
Прибыль 100 компаний - Мо=0+500*(41-1)/(41-1+41-32)=408.16 млн.
Оказывается, по расположению средней арифметической, моды и медианы можно судить о форме распределения. Если оно симметричное, то все три величины равны.
В практике мода и медиана иногда используются вместо средней арифметической или вместе с ней. Фиксируя средние цены товаров или продуктов на рынке записывают наиболее часто встречающуюся цену на рынке (моду цены).
Робастные характеристики для оценки среднего арифметического.
В ряде случаев в изучаемой совокупности имеется небольшое число элементов с чрезвычайно большим или чрезмерно малым значением исследуемого признака.
В этих случаях в дополнение к среднему арифметическому целесообразно вычислить моду и медиану, которые в отличие от среднего не зависят от крайних, не характерных для совокупности значений признака. Мода и медиана относятся к классу так называемых “робастных характеристик”, т.е. не чувствительных к аномальным значениям признака. Рассмотрим робастные характеристики, применяемые для оценки среднего арифметического:
1. усеченное среднееарифметическое порядка 
Пусть имеем ряд значений признака, упорядоченный в возрастающем порядке
, упорядоченный в возрастающем порядке. Пусть первые x(1),...,x(m) - аномально маленькие, x(n-m+1),...,x(n) - аномально большие.
- указывает долю отбрасываемых значений признака.
2. среднее по Виндору
Отличается от усеченного тем, что аномальные значения признака не отбрасываются, а полагаются крайним значениям, принимаемым на обработку.
x(1)=x(2)...=x(m)=x(m+1)
x(n)=x(n-1)=...=x(n-m+1)=x(n-m)