Остальные рефераты / Шпаргалка: Шпаргалка по Высшей математике 2

Шпаргалка: Шпаргалка по Высшей математике 2

Вопрос 1:Прямоугольная и полярная системы координат:

Две взаимно перпендикулярные оси Ох и Оу с общим началом координат О и одинаковой масштабной единицей составляют прямоугольную (декартову) систему координат на плоскости Оху . Эти оси называются осями координат, ось Ох – осью абсцисс, ось Оу – осью ординат.

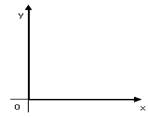
Разместим в пространстве координатную плоскость Оху так, чтобы ось ординат Оу лежала в плоскости чертежа и была направлена вправо, а ось Ох была направлена вниз и была перпендикулярна осям Оу и Оz. Из точки О – начала координат – перпендикулярно Оху вверх проведем ось Оz – ось аппликат. Если на всех осях взять одинаковую масштабную единицу, то получаем прямоугольную декартову систему координат в пространстве Оху z . Оси Ох, Оу, Оz называются координатными плоскостями.

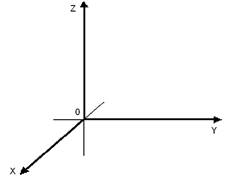
Полярная система координат.

Проведем из точки О – полюса – луч, который является полярной осью.

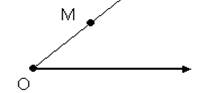
Положение любой точки на плоскости определяется парой чисел. Угол , на который нужно повернуть прямую О, чтобы она совпала с точкой М (поворот против чисовой стрелки). Полярный радиус – это длина отрезка ОМ.

М (;), при этом 02П, а 0+.

Совместим прямоугольную систему координат с полярной так, чтобы её начало совпадало с полюсом, а полярная ось - с осью абсцисс.

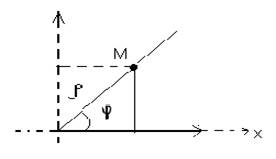
x = cos

y = sin

x² +y² =² (cos² +sin² )

Вопрос 2: Определение предела функции:

Определение набора тех множеств, в которые последовательно, при своём изменении в соответствии с рассматриваемым условием, попадает переменное ( или ), от которого зависит изменяющаяся величина ( или ). В случае условия эти множества имеют вид ; в случае - вид ; в случае - вид . Назовём их окончаниями базы предела при данном условии, а полный набор таких окончаний - базой предела. Базу предела будем обозначать так же, как само условие, а именно, , ,и т. п.

Таким образом,

Итак, база предела - это набор окончаний, которые должны удовлетворять таким свойствам: все они непусты и если и - два разных окончания (одной и той же базы), то база должна содержать третье окончание , которое содержится в каждом из первых двух: .

Определение: Пусть - некоторая база и функция определена во всех точках некоторого окончания базы (и, значит, определена во всех точках более далёких окончаний ). Число называется пределом функции по базе (или при базе ) и обозначается если для любого (сколь угодно малого) числа найдётся такое окончание базы , что при всех выполняется неравенство . Тот факт, что , записывают ещё в виде

Геометрический смысл данного определения предела таков: на плоскости , на которой нарисован график функции , проведём горизонтальную полосу ширины вокруг горизонтальной прямой . Тот факт, что , означает, что найдётся достаточно далёкое окончание базы , на котором график функции целиком лежит в этой полосе. При уменьшении ширины полосы окончание, возможно, придётся брать более далёким, но, всё равно, и в любую более узкую полосу умещается график на достаточно далёком окончании.