Шпаргалка: Шпаргалка по Высшей математике 2

Определение : Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c - его диагональю (рис. 10.2).

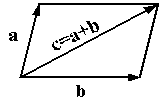
Рис.10.2.Сложение векторов

Сложение векторов в соответствии с рисунком 10.2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 1.3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.

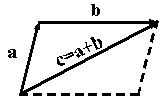
Рис.10.3.Правило треугольника

Определение : Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и .

Вектор, противоположный вектору a, обозначается , то есть .

Определение : Разностью векторов a и b называется сумма .

Разность обозначается , то есть .

Определение : Произведением вектора a на вещественное число называется вектор b, определяемый условием

1)и, если , то еще двумя условиями:

2) вектор b коллинеарен вектору a;

3) векторы b и a направлены одинаково, если , и противоположно, если .

Произведение вектора a на число обозначается (рис 1.4).

Рис.10.4.Умножение вектора на число

Замечание : Когда речь идет о связи векторов с числами, то иногда числа называют скалярами.

Теорема : Для любых векторов и любых вещественных чисел выполняются следующие свойства:
1)(свойство коммутативности операции сложения);
2) (свойство ассоциативности операции сложения);
3);
4);
5) (свойство ассоциативности по отношению к числам);
6) (свойство дистрибутивности по отношению к умножению на число);
7) (свойство дистрибутивности по отношению к умножению на вектор;
8) .

9) равенство верно тогда и только тогда, когда или , или ;
10) вектор, противоположный вектору a, равен , то есть ;
11) для любых векторов a и b существует такой вектор x, что .

Вопрос 2: Бесконечно малые и бесконечно большие:

Бесконечно малые и их основные свойства:

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно , если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Доказательство.

Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .

Если , то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.