Шпаргалка: Шпаргалка по Высшей математике 2

1) , где  - угол между векторами и ,

2) вектор ортогонален векторам и

3) , и образуют правую тройку векторов. Обозначается: или. Свойства векторного произведения векторов :

1) ;

2) , если  или = 0 или = 0;

3) (m)= (m) = m();

4) (+ ) = +  ;

5) Если заданы векторы (xa, ya, za) и (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами , то =

6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

Пример. Найти векторное произведение векторов и . = (2, 5, 1); = (1, 2, -3) .

Пример . Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0). (ед2).

Смешанное произведение векторов.

Определение. Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и . Обозначается или (, ,). Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .

Свойства смешанного произведения:

1)Смешанное произведение равно нулю, если: а)хоть один из векторов равен нулю; б)два из векторов коллинеарны; в)векторы компланарны.

2)

3)

4)

5) Объем треугольной пирамиды, образованной векторами , и , равен

6)Если , , то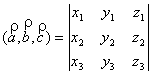

Пример . Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости. Найдем координаты векторов: 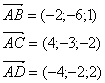Найдем смешанное произведение полученных векторов: 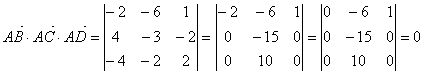, Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.

Вопрос 2: Первый замечательный предел:

Определение : Первым замечательным пределом называется предел

Теорема: Первый замечательный предел равен

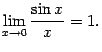
Доказательство . Рассмотрим два односторонних предела 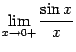и 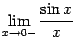и докажем, что каждый из них равен 1. Тогда по теореме двусторонний предел 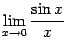также будет равняться 1.

Итак, пусть (этот интервал - одно из окончаний базы ). В тригонометрическом круге (радиуса ) с центром построим центральный угол, равный , и проведём вертикальную касательную в точке пересечения горизонтальной оси с окружностью (). Обозначим точку пересечения луча с углом наклона с окружностью буквой , а с вертикальной касательной -- буквой ; через обозначим проекцию точки на горизонтальную ось.

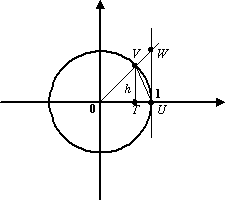
Рис.2.27.Тригонометрический круг