Учебное пособие: Методические указания и контрольные задания для студентов-заочников
,
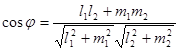- условие параллельности,
- условие перпендикулярности.
Здесь 
и 
- направляющие векторы прямых.
3. Пусть прямые L1 и L2 заданы уравнениями с угловыми коэффициентами
у = k1 x+b1 и y = k2 x + b2 , где 
, а α1 и α2 – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α2 - α1 . Тогда
.
Условие параллельности имеет вид: k1 =k2 ,
условие перпендикулярности – k2 =-1/k1 , поскольку при этом tgφ не существует.
Расстояние от точки до прямой.
Рассмотрим прямую L и проведем перпендикуляр ОР к ней из начала координат (предполагаем, что прямая не проходит через начало координат).
Расстояние от точки до прямой определяется так:
Замечание. Для того, чтобы привести общее уравнение прямой к нормальному виду, нужно умножить его на число 
, причем знак выбирается противоположным знаку свободного члена С в общем уравнении прямой. Это число называется нормирующим множителем.
Пример. Найдем расстояние от точки А(7,-3) до прямой, заданной уравнением
3х + 4у + 15 = 0. А² + B²=9+16=25, C=15>0, поэтому нормирующий множитель равен
-1/5, и нормальное уравнение прямой имеет вид: 
Подставив в его левую часть вместо х и у координаты точки А, получим, что ее отклонение от прямой равно
Следовательно, расстояние от точки А до данной прямой равно 4,8.
Расстояние между двумя точками М(х,у,z) и N( х1 ,у1 ,z1 ) выражается формулой
d(MN) = (х1 – x)² + (у1 – y)² + (z1 – z)²
Плоскость в пространстве.
A(x - x0 ) + B(y - y0 ) + C(z - z0 ) = 0.
уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
После приведения подобных можно записать уравнение в виде:
Ax + By + Cz + D = 0,
где D = -Ax0 - By0 - Cz0 . Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.
уравнение плоскости в отрезках.. Параметры а, b и с равны величинам отрезков, отсекаемых плоскостью на координатных осях.
Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.