Учебное пособие: Методические указания и контрольные задания для студентов-заочников
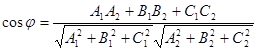
Условие параллельности плоскостей заключается в параллельности нормалей:
а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:
A1 A2 + B1 B2 + C1 C2 = 0
Прямая в пространстве.
Замечание. Прямую в пространстве невозможно задать одним уравнением. Для этого требуется система двух или более уравнений.
Первая возможность составить уравнения прямой в пространстве – представить эту прямую как пересечение двух непараллельных плоскостей, заданных уравнениями
A1 x+B1 y+C1 z+D1 =0 и A2 x+B2 y+C2 z+D2 =0, где коэффициенты A1 ,B1 ,C1 и A2 ,B2 ,C2 не пропорциональны:
A1 x+B1 y+C1 z+D1 =0 A2 x+B2 y+C2 z+D2 =0.
Однако при решении многих задач удобнее пользоваться другими уравнениями прямой, содержащими в явной форме некоторые ее геометрические характеристики.
Составим уравнения прямой, проходящей через точку М0 (x0 ,y0 ,z0 ) параллельно вектору a={l,m,n}.
Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.
Для любой точки М(x,y,z), лежащей на данной прямой, вектор М0 М = {x - x0 ,y - y0 ,z - z0 ) коллинеарен направляющему вектору а. Поэтому имеют место равенства:
называемые каноническими уравнениями прямой в пространстве.
В частности, если требуется получить уравнения прямой, проходящей через две точки:
М1 (х1 , у1 , z1 ) и M2 (x2 , y2 , z2 ), направляющим вектором такой прямой можно считать вектор М1 М2 = {x2 – x1 , y2 - y1 , z2 - z1 }, и уравнения (8.11) принимают вид:
-
- уравнения прямой, проходящей через две данные точки.
Если же принять каждую из равных дробей в уравнениях (8.11) за некоторый параметр t, можно получить так называемые параметрические уравнения прямой:
.
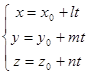Угол между прямыми. Угол между прямой и плоскостью.
Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида
и 
косинус угла между ними можно найти по формуле:
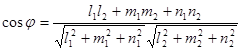. (8.14)
Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:
- условие параллельности прямых, (8.15)
- условие перпендикулярности прямых. (8.16)