Учебное пособие: Методичний матеріал по викладанню алгебри
Потім я доводжу це твердження в загальному вигляді ( тобто для будь-якого паралельного перенесення і довільних точок N і M ), показую на кодоскопі мал. 1.
Алгоритм доведення демонструю на кодоскопі.
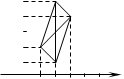
Нехай O1 – середина відрізка NM', а O2 – середина відрізка N'M. Знайти координати точок і.
Для O1 :
x = (x1 +x2 +a)/2, y = (y1 + y2 b)/2;
для O2 :
x = (x1 +a+x2 )/2, y = (y1 +y2 +b)/2.
Точки О1 =О2 – співпадають (одна і та ж точка).
Отже, діагональ чотирикутника N'NM'M перетинаються і точкою перетину є точка О (середина ); звідки слідує, що чотирикутник NN'M'M – паралелограм (мал. 2), тобто NN' || MM' і NN'=MM'.
y
![]() N(x1 +a;y1 +b)
N(x1 +a;y1 +b)
 5
5
M(x2 +a;y2 +b)
o
2 N
M 0 1 2 3 4 x
Мал. 2
Звертаю увагу учням на те, що ми довели наступне:
а) NM=N'M', тобто, що паралельне перенесення зберігає відстань між точками, а це означає – рух;
б) пряма переходить у паралельну пряму.
Пригадати з учнями теорему 9.4 (про існування і єдиності паралельного перенесення).
Підвести підсумок фронтального опитування й оголосити оцінки.
ІІ. Вивчення нового матеріалу.
Звертаю увагу учням на те, що ми повторили паралельне перенесення, яке тепер буде називатися по новому – вектор .
Після таких міркувань переходимо до означення вектора, яке подано у підручнику (п. 91).
Вектором називається напрямлений відрізок (за підручником мал. 215 демонструю на кодоскопу).
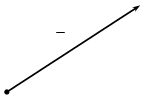 B
B
a
A