Учебное пособие: Методы коллокаций и Галеркина
Пусть дано дифференциальное уравнение с линейными краевыми условиями
![]() , (2.62)
, (2.62)
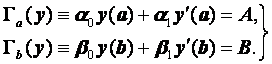 (2.63)
(2.63)
Будем искать приближенное решение этой краевой задачи в виде суммы
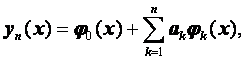 (2.64)
(2.64)
где ![]() – некоторая непрерывная функция, удовлетворяющая неоднородным краевым условиям (2.63), а
– некоторая непрерывная функция, удовлетворяющая неоднородным краевым условиям (2.63), а ![]() – какая-то система линейно независимых функций, удовлетворяющих однородным краевым условиям
– какая-то система линейно независимых функций, удовлетворяющих однородным краевым условиям
![]() (2.65)
(2.65)
и, кроме того функции ![]() при
при ![]() образуют в классе функций c 2 [a ,b ], удовлетворяющих условиям (2.65), полную систему.
образуют в классе функций c 2 [a ,b ], удовлетворяющих условиям (2.65), полную систему.
Заметим, что свойство полноты понимается следующим образом.
Обозначим через G класс функций y ( x ) , принадлежащих c 2 [a ,b ](то есть дважды непрерывно дифференцируемых на [a ,b ]) и удовлетворяющих граничным условиям (2.65). Говорят, что система функций ![]() полна в классе G , если для любого
полна в классе G , если для любого ![]() и любой функции
и любой функции ![]() можно указать такое n и такие параметры
можно указать такое n и такие параметры ![]() , что имеет место неравенство
, что имеет место неравенство
![]()
где 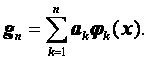
Это означает, что для любой допустимой функции ![]() найдется такая функция
найдется такая функция ![]() , которая на [a ,b ]будет сколь угодно точно приближать функцию y ( x ) вместе с ее производными
, которая на [a ,b ]будет сколь угодно точно приближать функцию y ( x ) вместе с ее производными ![]() и
и ![]() .
.
Докажем, что если для некоторой функции F ( x ) и полной системы функций ![]() выполняется соотношение ортогональности
выполняется соотношение ортогональности
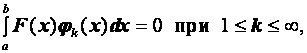 (2.66)
(2.66)
то функция ![]() . Для этого из полной системы
. Для этого из полной системы ![]() последовательной ортогонализацией построим полную ортогональную систему
последовательной ортогонализацией построим полную ортогональную систему ![]()
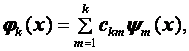
причем ![]() иначе
иначе ![]() были бы линейно зависимы. Разлагая по новой системе функцию F ( x ) , найдем
были бы линейно зависимы. Разлагая по новой системе функцию F ( x ) , найдем
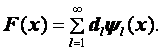
Подставляя это разложение в соотношение ортогональности (2.66), придем к равенству
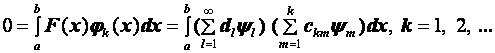 (2.67)
(2.67)
Вычислим последний интеграл:
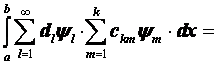
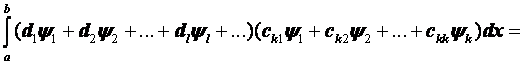
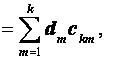 так как
так как 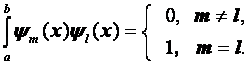
Таким образом, уравнение (2.67) принимает вид
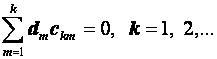 .
.
Полагая здесь k = 1, получим ![]() , и так как
, и так как ![]() , то
, то ![]() . Полагая k = 2, получим
. Полагая k = 2, получим ![]() , и так далее. Следовательно, все коэффициенты
, и так далее. Следовательно, все коэффициенты ![]() в разложении функции F ( x ) равны нулю и поэтому F ( x ) тождественно равна нулю, что и требовалось доказать.
в разложении функции F ( x ) равны нулю и поэтому F ( x ) тождественно равна нулю, что и требовалось доказать.
Возвращаясь теперь к задаче (2.62), (2.63), видим, что если бы мы нашли такую функцию y ( x ) , удовлетворяющую условиям (2.63), и чтобы ![]() было ортогонально
было ортогонально ![]() при любых
при любых ![]() , то это означало бы, что
, то это означало бы, что ![]() ,и задача (2.62), (2.63) была бы решена. Если же ортогональность есть только при
,и задача (2.62), (2.63) была бы решена. Если же ортогональность есть только при ![]() , то в разложении
, то в разложении ![]() по системе
по системе ![]() входят
входят ![]() и более старшие коэффициенты, то есть
и более старшие коэффициенты, то есть ![]()