Учебное пособие: Методы коллокаций и Галеркина

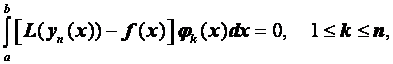(2.68)где

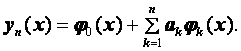
Это дает алгебраическую систему уравнений для определения коэффициентов a _k . Найдя из нее коэффициенты, получим приближенное решение.

Если оператор нелинейный, то система (2.68) тоже будет нелинейной и решение ее весьма затруднительно. Если же оператор линейный, то система (2.68) также будет линейной и можно решать задачу с большим числом коэффициентов.

В методе Галеркина функция должна удовлетворять краевым условиям (2.63). Поэтому можно выбрать в виде

,

и коэффициенты найти как решение системы уравнений

Таким же образом отыскиваются функции . Выберем, например, полную систему в виде многочленов последовательных степеней:

.

Коэффициенты найдем из однородных краевых условий (2.65)

(2.65^а )

при всех .

Так, для и условия (2.65^а ) принимают вид:

В этой системе из двух уравнений три неизвестных: и . Одну из них можно выбрать произвольно, положив, например, . Аналогично отыскивают коэффициенты для .

Для простых условий вида то есть функции можно вычислять по правилу

или

Отметим, что при нелинейном краевом условии вида, например, линейная комбинация (2.64) с произвольными коэффициентами a_k уже не будет удовлетворять этому краевому условию. Поэтому метод Галеркина применим только к задачам с линейными краевыми условиями, хотя допустим и нелинейный оператор L .

Пример 1. Методом Галеркина найти приближенное решение уравнения

с условиями

В качестве системы базисных функций выберем

Ограничимся четырьмя функциями , то есть k = 0, 1, 2, 3. Решение будем искать в виде