Учебное пособие: Методы решения краевых задач, в том числе "жестких" краевых задач

[ U∙ K(x←x) ] ∙ Y(x) = u - U∙ Y*(x←x) ,

Или получаем краевые условия, перенесенные в точку x:

U∙ Y(x) = u ,

где U= [ U∙ K(x←x) ] и u = u - U∙ Y*(x←x) .

Теперь уже к этой группе линейных алгебраических уравнений применяем построчное ортонормирование и получаем эквивалентное матричное краевое условие:

U∙ Y(x) = u.

И так далее.

И аналогично поступаем с промежуточными матричными краевыми условиями, переносимыми с правого края в рассматриваемую точку.

В итоге получаем систему линейных алгебраических уравнений с квадратной матрицей коэффициентов, состоящую из двух независимо друг от друга поэтапно проортонормированных матричных краевых условий, которая решается любым известным методом для получения решения Y(x) в рассматриваемой точке x:

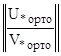∙ Y(x) = .

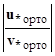5 Второй вариант метода «переноса краевых условий» в произвольную точку интервала интегрирования

Этот вариант метода еще не обсчитан на компьютерах.

Предложено выполнять интегрирование по формулам теории матриц [Гантмахер] сразу от некоторой внутренней точки интервала интегрирования к краям:

Y(0) = K(0←x) ∙ Y(x) + Y*(0←x) ,

Y(1) = K(1←x) ∙ Y(x) + Y*(1←x) .

Подставим эти формулы в краевые условия и получим:

U∙Y(0) = u,

U∙[ K(0←x) ∙ Y(x) + Y*(0←x) ] = u,

[ U∙ K(0←x) ] ∙ Y(x) = u - U∙Y*(0←x) .

и

V∙Y(1) = v,

V∙[ K(1←x) ∙ Y(x) + Y*(1←x) ] = v,

[ V∙ K(1←x) ] ∙ Y(x) = v - V∙Y*(1←x) .

То есть получаем два матричных уравнения краевых условий, перенесенные в рассматриваемую точку x:

[ U∙ K(0←x) ] ∙ Y(x) = u - U∙Y*(0←x) ,

[ V∙ K(1←x) ] ∙ Y(x) = v - V∙Y*(1←x) .

Эти уравнения аналогично объединяются в одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения решения Y(x) в любой рассматриваемой точке x:

∙ Y(x) = .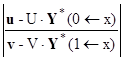

В случае «жестких» дифференциальных уравнений предлагается следующий алгоритм.