15) Критическая скорость передачи R_кр

R_кр === 393,102 [бод]

Оценка надёжности и эффективности дискретного канала связи

1. Оценка теоремы Шеннона по скорости

R<R_кр

749,8676> 393,102

2. Оценка выполнения теоремы по кодированию

H’(A) < C

970,3227 > 762,8716

3. Рекомендации по повышению надёжности и эффективности

Из-за невыполнения теоремы о скорости передачи невозможным становится восстановление исходного сообщения. При кодировании и декодировании информации вероятность ошибки может быть сколь угодно велика. Для улучшения эффективности необходимо увеличить емкость канала С.

Теоремы Шеннона не выполняются, а значит, наш канал связи не является эффективным и надежным.

Построение канальной матрицы объединения

Найдем безусловные вероятности появления сигналов на входе приемника по формуле:

Зная КМИ можно построить КМО: р(а_i, ,b_j )= p(a_i )p(b_j /а_i )

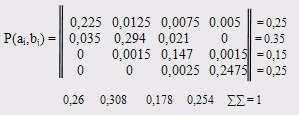
Построение канальной матрицы приемника

Зная КМО мы можем построить КМП, найдя элементы по формуле :

p(a_i / b_j )= p(a_i ,b_j )/p(b_j )

Часть 2. Теория кодирования

6. Оптимальное кодирование. Идея сжатия

Основной характеристикой дискретного канала связи является скорость передачи данных. При избыточности переданного сообщения скорость передачи уменьшается. Для исключения избыточности сообщения используют математические и программные средства компрессии данных без потери содержания информации, в том числе оптимальное кодирование.

Оптимальное кодирование применяют для того, чтобы:

· сжимать данные (компрессия);

· снижать время передачи данных при той же скорости передачи;

· уменьшить возможные потери и искажения данных;

· архивировать данные, эффективно использовать память.

Основная идея оптимального кодирования лежит в том, что символам сообщения, которые имеют большую вероятность, присваивают короткие бинарные коды, то есть образуются бинарные кодовые слова разной длины – неравномерные коды. Оптимальным неравномерным кодом (ОНК) называется такой код, для которого средняя длина кода есть минимальной.

Такая идея сжатия была применена в азбуке Морзе, где наиболее встречающимся символам соответствовали наиболее короткие коды. Сам алфавит состоял из точек и тире.

6.1 Равномерный двоичный код (РДК), корневое бинарное дерево РДК, длина кода РДК, сообщение в РДК