Учебное пособие: Расчет информационных характеристик дискретного канала

[бит/символ]

4. Информационные характеристики приемника сообщений

4.1Количество информации приёмника

Количество информации

Количеством информации символа сообщения определяется:

I(b_j ) = - log₂ (p(b_j )) = - log(p(b_j )) [бит] (j=1,2…n)

В Шенноновской теории информации количество информации приемника определяется вероятностью появления символа.

I(b_j ) = - ln(p(b_j )) [нат]

I(b_j ) = - lg(p(b_j )) [дит]

Каждый символ сообщения содержит своё количество информации.

Свойства количества информации приемника сообщений

1. Количество информации неотрицательно: I(b_j ) ≥ 0

2. Чем выше вероятность, тем меньшее количество информации содержит символ.

3. Если вероятность символа равна 1, то количество информации этого символа равно 0.

р(b_j ) = 1 ⇒I(b_j ) = 0

4. Аддитивность. Количество информации нескольких символов равно сумме количеств информаций каждого.

I(b_1, b_2, b₃ ) = I(b₁ ) + I(b₂ ) + I(b₃ )

Энтропия – среднее количество информации на символ сообщения (средневзвешенное).

[бит/символ]

Свойства энтропии

1. Энтропия неотрицательна:

Н(А) ≥ 0

2. Энтропия равна нулю тогда и только тогда, когда вероятность символа равна 1:

Н(a_i ) = 0 ⇔р(a_i ) =1

3. Энтропия ограничена

H (B) =< log n[бит/символ]

где n – количество символов в сообщении.

4. Максимальная энтропия равна

H_max (B) = log n[бит/символ]

4.2Информационные потери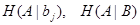

Существует два вида условной энтропии, которые определяют действия помех на дискретном канале – это частная условная энтропия (ЧУЭ) и общая условная энтропия (ОУЭ).

Частная условная энтропия приемника (ЧУЭП) сообщений определяет потери информации каждого принятого сигнала _.