Учебное пособие: Теорема Остроградського-Гаусса, потенціальний характер електростатичного поля та діелектрики в електричному полі

Вступ

Обчислення напруженості поля системи електричних зарядів з допомогою принципу суперпозиції електростатичних полів можливо значно спростити, використовуючи вивчену німецьким ученим К. Гауссом теорему, що визначає потік вектора напруженості електричного поля через довільну замкнену поверхню (загальне визначення потоку для будь-якого вектора було дано Полтавським математиком Остроградським).

На основі теореми розраховується електричне поле для заряджених тіл, що мають симетрію.

Поняття потоку вектора електричного зміщення

Нехай в однорідному електричному полі розміщена площина D S так, що вектор зміщення утворює з нормаллю кут a (рис. 1).

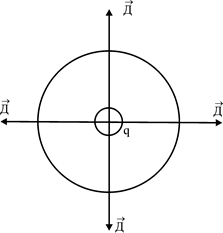
Рис. 1

Потоком вектора зміщення називається добуток нормальної складової цього вектора (поверхні) і величини площадки

але , тому маємо або .

Якщо поле неоднорідне, то поверхнею розбивають на нескінченно малі ділянки.

Тоді .

А потік через всю довільну поверхню визначиться

Теорема Гауса-Остроградського і її застосування для розрахунку електричних полів

Спочатку розрахуємо потік вектора напруженості поля точкового заряду q через сферичну поверхню радіусом r .

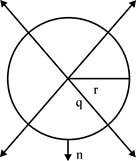
Рис. 2

Потік вважається додатнім; якщо лінії напруженості виходять із поверхності і від’ємним для ліній, що входить у поверхню. Напруженість поля в точках сферичної поверхні стала по величині дорівнює:

Вектори напруженості поля у всіх точках співпадають з напрямком нормалі.

Тому потік вектора напруженості через сферичну поверхню дорівнює

Підставимо значення Е і S .

;

Таким чином потік вектора напруженості поля точкового заряду q через сферичну поверхню пропорційний q .

Цей висновок узагальнюється теоремою Гауса – Остроградського на будь-яку систему зарядів, оточених довільно замкненою поверхнею.

Теорема. Потік вектора електричної напруженості через будь-яку замкнену поверхню пропорційний алгебраїчній сумі зарядів, охоплюваних цією поверхнею.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--