Учебное пособие: Теорема Остроградського-Гаусса, потенціальний характер електростатичного поля та діелектрики в електричному полі

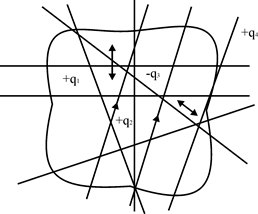
Рис. 3

Як бачимо з рисунку 3 заряди і створюють додатки потоку, а від’ємний потік через замкнуту поверхню: тому повний потік вектора напруженості через цю поверхню дорівнює

.

Заряд , що знаходиться поза замкнутою поверхнею потоку через неї не створює.

У загальному випадку теорема Остроградського – Гауса запишеться:

Вектор зміщення в точках сферичної поверхні має вираз:

,

а його потік через цю поверхню дорівнює:

; .

Для вектора зміщення теорема Гауса – Остроградського формулюється: потік вектора зміщення через будь-яку замкнуту поверхню дорівнює алгебраїчній сумі зарядів, охоплених цією поверхнею:

В системі СІ потік вектора зміщення вимірюється в Кл.

Із теореми Гауса маємо ряд наслідків:

1) Лінії напруженості починаються на позитивних і закінчуються на негативних зарядах.

2) Повний потік вектора зміщення через поверхню, що охоплює систему зарядів алгебраїчна сума яких дорівнює нулю.

3) Якщо замкнута поверхня не охоплює електричні заряди, то потік через неї дорівнює нулю, число ліній напруженості, що входять дорівнює числу ліній напруженості, що виходять:

а) Поле рівномірно зарядженої нескінченої пластини.

Хай пластинка заряджена позитивно з поверхневою густиною

Із симетрії поля випливає, що лінії напруженості перпендикулярні до пластинки (рис. 4).

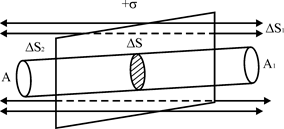
Рис. 4

Вибираємо довільно точку А і симетричну їй . Проводимо циліндричну поверхню так, щоб в основах її знаходились точки А і , а лінії напруженості були паралельні твірним.

Тоді потік через бокову поверхню дорівнюватиме О. Повний потік буде дорівнювати сумі потоків через основи

Заряд, що охоплюється циліндричною поверхнею дорівнює s × D S .

Використовуючи теорему Гауса одержимо: