Учебное пособие: Вычислительная математика
Решение задачи y* называется устойчивым по исходным данным x* , если оно зависит от исходных данных непрерывным образом. Это означает, что малому изменению исходных данных соответствует малое изменение решения. Строго говоря, для любого e > 0 существует d = d (e ) > 0 такое, что всякому исходному данному x* , удовлетворяющему условию |x - x* | < d , соответствует приближенное решение y* , для которого |y – y* | < e .
Говорят, что задача поставлена корректно , если выполнены следующие три условия:
1. Решение существует при любых допустимых исходных данных.
2. Это решение единственно.
3. Это решение устойчиво по отношению к малым изменениям исходных данных.
Если хотя бы одно из этих условий не выполнено, задача называется некорректной.
Пример 1.1.
Покажем, что задача вычисления определенного интеграла I = 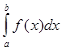 корректна. Пусть f * (x ) – приближенно заданная функция и I * =
корректна. Пусть f * (x ) – приближенно заданная функция и I * = 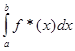 . Очевидно, приближенное решение I * существует и единственно. Определим абсолютную погрешность f * с помощью равенства D(f* ) =
. Очевидно, приближенное решение I * существует и единственно. Определим абсолютную погрешность f * с помощью равенства D(f* ) = ![]() |f (x ) – f* (x )|. Так как
|f (x ) – f* (x )|. Так как
D(I ) = |I – I* | = |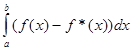 | £ (b – a )D(f* ),
| £ (b – a )D(f* ),
то для любого e > 0 неравенство D(I ) < e будет выполнено, если будет выполнено условие D (f* ) < d , где d = e / (b – a ).
Таким образом, решение I * устойчиво. Все три условия корректности задачи выполнены.
Пример 1.2.
Покажем, что задача вычисления производной u (x ) = f ' (x ) приближенно заданной функции некорректна.
Пусть f * (x ) – приближенно заданная на отрезке [a , b ] непрерывно дифференцируемая функция и u* (x ) = (f* (x ))' . Определим абсолютные погрешности следующим образом: D(f* ) = ![]() |f (x ) – f* (x )|, D(u* ) =
|f (x ) – f* (x )|, D(u* ) = ![]() |u (x ) – u* (x )|.
|u (x ) – u* (x )|.
Возьмем, например, f* (x ) = f (x ) + a sin (x/ a 2 ), где 0 < a < 1. Тогда, u* (x ) = u (x ) + a - 1 cos (x/ a 2 ), D(u* ) = a - 1 , т. е. погрешность задания функции равна a , а погрешность производной равна a - 1 . Таким образом, сколь угодно малой погрешности задания функции f может отвечать сколь угодно большая погрешность производной f '.
1.3 Вычислительные методы
Под вычислительными методами будем понимать методы, которые используются в вычислительной математике для преобразования задач к виду, удобному для реализации на ЭВМ. Подробнее с различными классами вычислительных методов можно познакомиться, например, в [1]. Мы же рассмотрим два класса методов, используемых в нашем курсе.
1. Прямые методы. Метод решения задачи называется прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. Наименование элементарной операции здесь условно. Это может быть, например, вычисление интеграла, решение системы уравнений, вычисление значений функции и т. д. Важно то, что ее сложность существенно меньше, чем сложность основной задачи. Иногда прямые методы называют точными, имея в виду, что при отсутствии ошибок в исходных данных и при выполнении элементарных операций результат будет точным. Однако, при реализации метода на ЭВМ неизбежны ошибки округления и, как следствие, наличие вычислительной погрешности.
2. Итерационные методы. Суть итерационных методов состоит в построении последовательных приближений к решению задачи. Вначале выбирают одно или несколько начальных приближений, а затем последовательно, используя найденные ранее приближения и однотипную процедуру расчета, строят новые приближения. В результате такого итерационного процесса можно теоретически построить бесконечную последовательность приближений к решению. Если эта последовательность сходится (что бывает не всегда), то говорят, что итерационный метод сходится. Отдельный шаг итерационного процесса называется итерацией.
Практически вычисления не могут продолжаться бесконечно долго. Поэтому необходимо выбрать критерий окончания итерационного процесса. Критерий окончания связан с требуемой точностью вычислений, а именно: вычисления заканчиваются, когда погрешность приближения не превышает заданной величины.
Оценки погрешности приближения, полученные до вычислений, называют априорными оценками (от лат. a'priori – "до опыта"), а соответствующие оценки, полученные в ходе вычислений называют апостериорными оценками (от лат. a'posteriori – "после опыта").
Важной характеристикой итерационных методов является скорость сходимости метода. Говорят, что метод имеет p -ый порядок сходимости если
|x n+1 - x * | = C|x n - x * |p ,
где x n и x n+1 – последовательные приближения, полученные в ходе итерационного процесса вычислений, x * – точное решение, C – константа, не зависящая от n . Говорят, что метод сходится со скоростью геометрической прогрессии со знаменателем q < 1, если для всех n справедлива оценка:
|x n - x * | £ Cqn .
Итерационный процесс называется одношаговым , если для вычисления очередного приближения x n+1 используется только одно предыдущее приближение x n и k –шаговым, если для вычисления x n+1 используются k предыдущих приближений x n-k+1 , x n-k+2 , …, x n .
Тема 2. Решение нелинейных уравнений
2.1 Постановка задачи
Пусть дана некоторая функция f (x ) и требуется найти все или некоторые значения x , для которых
f (x ) = 0. (2.1)
Значение x * , при котором f (x * ) = 0, называется корнем (или решением ) уравнения (2.1).
Относительно функции f (x ) часто предполагается, что f (x ) дважды непрерывно дифференцируема в окрестности корня.