Дипломная работа: Численное решение уравнения Шредингера средствами Java

Обычно определяют (Дирака) следующим образом:

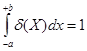
(4.4)

Из этих уравнений следует, что

(4.5)

для любой функции , в случае если интервал интегрирования включает точку .

Проделанные выше операции над интегралами Фурье показали, что

(4.6)

Это интегральное представление функции.

Дельта – функцию можно использовать, чтобы выразить важный интеграл 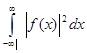через преобразование Фурье (4.1) от :

(4.7)

Это равенство называется теоремой Парсеваля. Она полезна для понимания физической интерпретации преобразования Фурье для , если известен физический смысл .

Предположим, что четная функция. Тогда

Заметим теперь, что -- также четная функция. Поэтому

(4.9)

Функция и ,определенные теперь только для положительных и , называются косинус - преобразованиями Фурье по отношению друг к другу.

Рассматривая преобразования Фурье нечетной функции, получаем аналогичные соотношения Фурье между синус - преобразованиями Фурье:

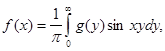
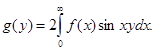(4.10)

Если нужно, можно симметризовать выражения, поставив множитель перед каждым интегралом (4.7)-(4.10). [4]

2.3 Метод аппроксимации оператора эволюции (split-operator method)

Рассмотрим более подробно другой метод аппроксимации оператора эволюции, в котором отсутствуют недостатки, свойственные рассмотренной выше схеме. Здесь оператор эволюции аппроксимируется симметричным расщеплением оператора кинетической энергии (split-operator method)

(5.1)

Основная погрешность данной аппроксимации связана с некоммутативностью операторов кинетической и потенциальной энергии. Вычисление действия такого оператора на волновую функцию включает следующие шаги. Преобразованная в импульсное представление волновая функция умножается на и преобразуется обратно в координатное представление, где умножается на . Полученный результат снова преобразуется в импульсное представление, умножается на преобразуется обратно в координатное представление. На этом один шаг по времени завершается. Переход от одного представления к

другому осуществляется посредством преобразования Фурье.

В данной курсовой работе используется Гауссов волновой пакет вида , а также ступенчатый потенциал. Сначала преобразуем нашу волновую функцию из координатного представления в импульсное

,(5.2)