Дипломная работа: Численный метод расчета нестационарных режимов гидравлических систем

Выражаем из (7) и подставляем в (8), получаем разностное уравнение:

Это уравнение можно записать в виде:

где:

.

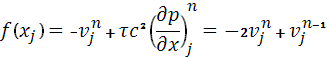Для решения уравнения (9) используем следующий способ дискретизации задачи [6].

Введем на отрезке [0,1] сетку с узлами 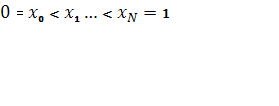в общем случае с неравномерным шагом .

Решение уравнения (9) будем искать например как решение задачи (преобразование Риккати)

Тогда для прогоночных коэффициентов и получим следующие уравнения:

С учетом того, что начальные условия для прогоночных коэффициентов в узлах и заранее неизвестны, вместо (10) рассматривается следующее уравнение для :

В отличии от уравнения (10) в (11) содержится дополнительное слагаемое, в котором есть дополнительный прогоночный коэффициент, а параметр определяется как линейная комбинация значений и в виде:

так, что (12) при обращается в тождество. Тогда для вычисления прогоночных коэффициентов получаем следующие задачи

Отметим, что начальные значения для уравнений (15)-(17) , , являются свободными параметрами и могут быть выбраны специальным образом с учетом свойств решения этих уравнений.

Наряду с уравнением (13) на отрезке рассмотрим уравнение

в котором прогоночные коэффициенты , , и параметр определяются аналогично предыдущему, но при задании начальных условий на правом конце отрезка, т.е. в точке . В результате аналогично (14) получим

и, кроме того,