Остальные рефераты / Дипломная работа: Численный метод расчета нестационарных режимов гидравлических систем

Дипломная работа: Численный метод расчета нестационарных режимов гидравлических систем

2) .

Начальные условия: .

Граничные условия: при

при

3) .

Начальные условия:.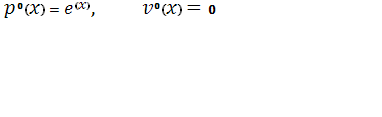

Граничные условия: при

при

Таблицы погрешностей

Расчеты на момент времени .

1) Для первого случая:

		Сплайн Эрмита		Формула трапеций
tau	h	Общая погрешность	Погрешность по h	Общая погрешность	Погрешность по h
0,1	0,1	0,832851872281	0,000005587977	0,883060158026	0,049862541589
	0,05	0,832846634174	0,000000349870	0,845471064588	0,012273448151
	0,025	0,832846305931	0,000000021627	0,836006949938	0,002809333501
	0,0125	0,832846285402	0,000000001098	0,833636730148	0,000439113711
0,05	0,1	0,411112170340	0,000014415426	0,555115166343	0,142993370234
	0,05	0,411098669010	0,000000914096	0,447750454263	0,035628658154
	0,025	0,411097811602	0,000000056688	0,420301941958	0,008180145849
	0,0125	0,411097757795	0,000000002881	0,413401372060	0,001279575951
0,025	0,1	0,201166720391	0,000030952418	0,635665878379	0,431272044005
	0,05	0,201137819976	0,000002052003	0,316227793596	0,111833959222
	0,025	0,201135896782	0,000000128809	0,230331588708	0,025937754334
	0,0125	0,201135774540	0,000000006567	0,208461455105	0,004067620731

2) Для второго случая:

		Сплайн Эрмита		Формула трапеций
tau	h	Общая погрешность	Погрешность по h	Общая погрешность	Погрешность по h
0,1	0,1	0,0363862195882	0,0000003533755	0,0365225558362	0,0001361850555
	0,05	0,0363858866179	0,0000000204052	0,0364193116294	0,0000329408486
	0,025	0,0363858674276	0,0000000012149	0,0363940756462	0,0000077048655
	0,0125	0,0363858662825	0,0000000000698	0,0363878963462	0,0000015255654
0,05	0,1	0,0193290379468	0,0000003902564	0,0197702772371	0,0004398989059
	0,05	0,0193286704260	0,0000000227356	0,0194417061597	0,0001113278285
	0,025	0,0193286490606	0,0000000013702	0,0193567096123	0,0000263312812
	0,0125	0,0193286477694	0,0000000000790	0,0193356062043	0,0000052278731
0,025	0,1	0,0098628022883	0,0000008650402	0,0110834356765	0,0012156369665
	0,05	0,0098619896672	0,0000000524191	0,0102244373458	0,0003566386358
	0,025	0,0098619404102	0,0000000031621	0,0099557308589	0,0000879321489
	0,0125	0,0098619374304	0,0000000001824	0,0098854427220	0,0000176440120

3) Для третьего случая:

		Сплайн Эрмита		Формула трапеций
tau	h	Общая погрешность	Погрешность по h	Общая погрешность	Погрешность по h
0,1	0,1	0,0503848043379	0,0000001782382	0,0505305705713	0,0001453810399
	0,05	0,0503846356429	0,0000000095432	0,0504215935780	0,0000364040466
	0,025	0,0503846266571	0,0000000005574	0,0503937716362	0,0000085821047
	0,0125	0,0503846261316	0,0000000000319	0,0503868920084	0,0000017024770
0,05	0,1	0,0276662900907	0,0000004434286	0,0284799145762	0,0008107561790
	0,05	0,0276658723062	0,0000000256441	0,0278803276463	0,0002111692492
	0,025	0,0276658481883	0,0000000015263	0,0277194379421	0,0000502795450
	0,0125	0,0276658467498	0,0000000000877	0,0276791571079	0,0000099987108
0,025	0,1	0,0143508893578	0,0000011533406	0,0175269261320	0,0031636285406
	0,05	0,0143498065190	0,0000000705018	0,0151730530598	0,0008097554684
	0,025	0,0143497402744	0,0000000042572	0,0145658072176	0,0002025096262
	0,0125	0,0143497362628	0,0000000002455	0,0144040736398	0,0000407760484

Замечание

1) Погрешность по вычислялась путем, взятия разности, между общей погрешностью и погрешности по времени. Погрешностью по времени мы считаем общую погрешность при минимальном .

2) С уменьшением шага наблюдается увеличение погрешности по , это связано с зависимостью показателя диагонального преобладания от шага .

Выводы

· В данной работе для решения начально-краевой задачи гиперболической системы дифференциальных уравнений была реализована схема с 4м порядком точности по пространственной переменной и 1м порядком по времени.

· Проведены исследования монотонности и устойчивости разностной схемы для линейной гиперболической системы второго порядка.

К-во Просмотров: 347

Бесплатно скачать Дипломная работа: Численный метод расчета нестационарных режимов гидравлических систем

>>> Скачать <<<