Дипломная работа: Дифференциальная геометрия поверхностей Каталана

Пусть - гладкая поверхность, – ее векторное параметрическое уравнение и .

Определение 1.1.

Первой квадратичной формой на поверхности называется выражение

(1)

Распишем это выражение подробнее.

,

Откуда (2)

Выражение (2) в каждой точке поверхности представляет собой квадратичную форму от дифференциалов и . Первая квадратичная форма является знакоположительной, так как ее дискриминант

и .

Для коэффициентов первой квадратичной формы часто используют следующие обозначения (и мы в своих исследованиях будем придерживаться именно их) ([1].[2],[3]):

,

,

.

Так что выражение (2) для формы можно переписать в виде

(3)

Соответственно,

.

1.2 Внутренняя геометрия поверхности

Известно, что, зная первую квадратичную форму поверхности, можно вычислять длины дуг кривых на поверхности, углы между кривыми и площади областей на поверхности. В самом деле, если рассмотреть формулы, определяющие вышеуказанные величины, можно заметить, что туда входят только лишь коэффициенты , , первой квадратичной формы. Поэтому если известная первая квадратичная форма поверхности, можно исследовать геометрию на поверхности, не обращаясь к ее уравнениям, а лишь используя ее первую квадратичную форму.

Совокупность геометрических фактов, относящихся к поверхности, которые можно получить при помощи ее первой квадратичной формы, составляет так называемую внутреннюю геометрию поверхности.

Поверхности, имеющие одинаковые первые квадратичные формы и потому имеющие одинаковую внутреннюю геометрию, называются изометричными.

Рассмотрим простой пример.

Пусть задана поверхность

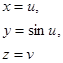
Это цилиндрическая поверхность с синусоидой в качестве направляющей.

Имеем:

,