Дипломная работа: Дифференциальная геометрия поверхностей Каталана

,

,

Следовательно,

.

Если сделать замену, вводя новые параметры и таким образом

,

.

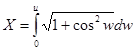Тогда первая квадратичная форма поверхности примет, очевидно, вид

.

Мы видим, что в новых переменных первая квадратичная форма рассматриваемой цилиндрической поверхности совпадает с первой квадратичной формой плоскости и поэтому внутренняя геометрия этой поверхности совпадает с внутренней геометрией плоскости. Т.е. синусоидальный цилиндр изометричен плоскости. Этот важный факт мы еще получим несколько другим способом.

Чисто геометрически это свойство понятно: синусоидальный цилиндр получается изгибанием (т.е. деформацией без сжатий и растяжений) обычной плоскости. При такой деформации внутренняя геометрия не изменяется.

Более того, можно показать, что если одна поверхность получается из другой путем изгибания, то внутренние геометрии этих поверхностей совпадают.

1.3 Вторая квадратичная форма поверхности

1.3.1. Определение второй квадратичной формы.

Основным объектом рассмотрения в этой части изложения станет - регулярная поверхность , заданная своим радиус-вектором.

,

В каждой точке такой поверхности помимо единичного вектора нормали

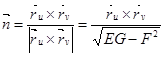(1)

Определен и второй дифференциал радиус вектора

(2)

Определение 1.2.

Второй квадратичной формой поверхности называется скалярное произведение векторов и .

([1],[3],[4],[5]) (3)

Нетрудно заметить, что в каждой точке поверхности квадратичная форма (3) является квадратичной формой относительно дифференциалов и .

Для коэффициентов второй квадратичной формы приняты (и мы также в дальнейшем будем пользоваться этим) следующие обозначения

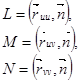(4)

Это позволяет записать ее в следующем простом виде

(5)