Дипломная работа: Графічні методи розвязування задач із параметрами

лінійна функція (де - змінні, - параметри);

лінійне рівняння (де - змінна, - параметри);

рівняння першої степені (де - змінна, - параметри, );

квадратне рівняння (де - змінна, - параметри, );

До задач з параметрами, які розглядаються в курсі середньої школи, можна

віднести, наприклад, пошук розв’язків лінійних та квадратних рівнянь в загальному виді, дослідження кількості їх коренів в залежності від значень параметрів

Природно, що такий невеликий клас задач багатьом учням не дозволяє усвідомити головне: параметр (фіксоване, але невідоме число) має двоїсту природу. По-перше, параметр можна розглядати як число, а по-друге, - це невідоме число. Таким чином, ділення на вираз, який містить параметр, добування кореня парного ступеня із таких виразів потребує попередніх досліджень. Як правило, результати досліджень впливають і на розв’язок, і на відповідь.

Головне, що необхідно усвідомити при роботі з параметром - це необхідність обережного відношення до фіксованого, але невідомого числа.

Дипломна робота присвячена розробці методики викладання теми “Графічні методи розв’язування задач з параметрами”.

Робота складається із вступу, 3 розділів та списку використаної літератури. Кожний із 3 розділів присвячений одному із графічних прийомів. Розділи діляться на параграфи. Кожний параграф побудовано за такою структурою. На початку параграфа наводиться необхідний теоретичний матеріал, потім даються задачі із подробним розв’язанням, а наприкінці наведені задачі для самостійної роботи з відповідями.

І розділ роботи “Координатна площина " присвячений побудові графічного образу на координатній площині .

ІІ розділ роботи “Координатна площина " присвячений побудові графічного образу на координатній площині .

ІІІ розділ роботи “Застосування похідної” присвячений побудові графічного образу із застосуванням похідної.

Дипломна робота може бути використана вчителями та студентами старших курсів при проведенні педагогічної практики.

Розділ 1. Координатна площина

На площині функція задає сім’ю кривих, які залежать від параметра . Кожній сім’ї функцій властиві деякі властивості. Нас буде цікавити питання: за допомогою якого перетворення площини (паралельний перенос, поворот, гомотетія і т.д.) можна перейти від однієї кривої сім’ї до будь-якої іншої. Кожному з таких перетворень буде присвячено окремий підрозділ.

Не завжди графічний образ сім’ї функцій описується простим перетворенням. Тому в таких ситуаціях необхідно зосередити увагу не на тому, як пов’язані криві однієї сім’ї, а на самі криві. Іншими словами, можна виділити ще один тип задач, в яких ідея розв’язку перш за все заснована на властивостях конкретних геометричних фігур, а не властивостях сім’ї взагалі. Нас будуть цікавити прямі та параболи. Такий вибір обумовлено окремим (основним) положенням лінійної та квадратичної функції в шкільній математиці.

Говорячи про графічні методи, неможливо обійти одну проблему, породжену практикою конкурсних екзаменів. Мається на увазі питання про законність розв’язку, який заснований на графічних зображеннях. З формальної точки зору результат, який “знятий" з рисунку, знайдений нестрого. Але вимоги до рівня математичної строгості для учня повинні визначатися здоровим глуздом.

Побудова графічних образів в даній роботі заснована на побудові графіків виду за допомогою перетворень графіка функції .

1.1 Паралельний перенос

Почнемо з задач, в який членами сім’ї кривих будуть прямі.

1. Для кожного значення параметра а визначити число розв’язків рівняння .

Розв’язання. Побудуємо графіки функцій та .

З рисунка 1.1.1 випливає, що при - розв’язків немає, при - 2 розв’язки, при - 4 розв’язки, при - 3 розв’язки, при - 2 розв’язки.

Рис.1.1.1

Відповідь: при - розв’язків немає, при - 2 розв’язки, при - 4 розв’язки, при - 3 розв’язки, при - 2 розв’язки.

2. Для кожного значення параметра визначити число розв’язків рівняння .

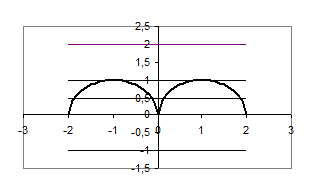
Розв’язання. Побудуємо графік функції . Знайдемо ОДЗ функції , тобто .

З рисунка 1.1.2 випливає, що при - розв’язків немає, при - 3 розв’язки, при - 4 розв’язки, при - 2 розв’язки, при - немає розв’язків.