Дипломная работа: Графічні методи розвязування задач із параметрами

Розв’язання. Перше рівняння системи зручно представити у вигляді . Це рівняння задає сім’ю кіл постійного радіуса, рівного 1, причому центри кіл лежать на прямій . Побудуємо графік функції (рис.1.1.18). На цьому ж рисунку показано чотири положення кола, при яких початкова система має єдиний Розв’язання.

Кожному з відмічених кіл відповідає деяке значення параметра с. Оскільки умова задачі вимагає, щоб с було найменшим, то з чотирьох кіл треба вибрати те, абсциса центра якого приймає найменше значення. Очевидно це буде коло з центром в точці О .

Рис.1.1.18

Маємо . З . Звідси . Тоді з . Таким чином, . Оскільки положенню центра О відповідає , то знаходимо

Відповідь:

9. При яких а множиною розв’язків нерівності є відрізок довжиною ?

Розв’язання. Графіком функції є півколо з радіусом, рівним 1, яке "пливе" своїм центром по вісі абсцис. Дана нерівність буде мати Розв’язання тоді, коли точки півкола будуть вище відповідних точок прямої . На рис.1.1.19 показано одно з можливих положень півкола.

Рис.1.1.19

Для цього випадку розв’язком початкової нерівності буде відрізок . Умова вимагає, щоб .

Якщо центр О₁ співпадає з точкою A (-1; 0) або розташований ліворуч, то розв’язком нерівності буде відрізок довжиною 2. Разом з тим, якщо О співпадає з точкою O (0; 0) або знаходиться праворуч, то розв’язком нерівності буде відрізок довжиною менше, ніж , або взагалі розв’язків не буде. Дійсно, якщо О₁ співпадає зО, то , a x - корінь рівняння Звідси та . Таким чином, потрібне положення центра О визначається умовою , тобто .

Знайдемо значення x та x. Очевидно x - найменший корінь рівняння

. Звідси . В той же час х - корінь рівняння Це рівняння рівносильне системі

Знайдене рівняння при має тільки один невід’ємний корінь, тобто.

За умовою . Розв’язав це рівняння, знаходимо , . Оскільки , то .

Відповідь: .

10 . Знайти всі значення параметра а, при яких рівняння має єдиний розв’язок.

Розв’язання. Представимо рівняння у вигляді . Права частина цього рівняння задає нерухомий "кут", ліва - "кут", вершина якого рухається по вісі абсцис (рис.1.1.20).

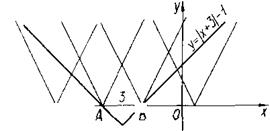
Рис.1.1.20

Рівняння буде мати єдиний розв’язок, якщо вершина рухомого "кута"

потрапить або в точку А або в точку В.

Маємо А ( -4; 0), В ( -2; 0), і координати цих точок задовольняють рівнянню . Тоді або . Звідси або .

Відповідь: або .

11 . Знайти всі значення параметра а, для яких найменше значення функції більше 2.

Розв’язання. Дана функція не задає сім’ю "кутів". За умовою задачі необхідно шукати значення параметра, при яких нерівність виконується при будь-яких х. Це і є формулювання, рівносильна даній.

Одержану нерівність слід переписати так: .